RAPPEL THÉORIQUE

L’objectif de l’analyse de variance à plan factoriel est de tester l’effet de deux ou de plusieurs variables indépendantes catégorielles (facteurs) sur une variable dépendante (VD) à l’intérieur d’une seule analyse (d’un seul modèle). Cette technique permet de calculer l’effet simple de chaque variable indépendante ainsi que leur interaction.

Cette section traite uniquement de l’ANOVA dit univarié car il porte sur une seule variable dépendante. Il est possible de créer un modèle factoriel avec plus d’une variable dépendante, appelé MANOVA (multivariate analysis of variance). D’autres modèles d’ANOVA existent, entre autres les modèles à mesures répétées qui permettent de combiner des variables dépendantes mesurées auprès du même échantillon. Ces modèles de la famille ANOVA seront présentés dans des sections futures. Entretemps, le lecteur est invité à consulter le livre d’Andy Field qui fait bien le tour de la question.

L’exemple de cette section présente un devis factoriel à deux facteurs. Le modèle est constitué des facteurs SEXE et DOMAINE (domaine d’étude) et de la variable dépendante SALAIRE. Comme chercheurs, nous voulons savoir de quelle manière le sexe (SEXE) et le domaine d’études (DOMAINE) sont associés avec le salaire de départ (SALAIRE).

Le devis factoriel

Ce devis comprend minimalement deux variables catégorielles appelées aussi « facteurs », d’où le nom de l’analyse. En raison de la complexité de l’interprétation des interactions multiples, les modèles factoriels incluent rarement plus de trois facteurs.
De plus, les modèles ainsi créés sont catégorisés en fonction des niveaux des facteurs, c’est-à-dire le nombre de catégories contenu dans chaque variable indépendante. Ainsi, on dirait que le modèle factoriel de l’exemple décrit plus haut est un modèle factoriel dit « 2×3 » car la variable SEXE comprend 2 catégories (1 = homme, 2 = femme) et la variable DOMAINE comprend 3 catégories (1 = soins infirmiers, 2 = éducation à l’enfance, 3 = génie civil).

Hypothèse nulle

Dans l’exemple d’un modèle à deux facteurs, l’hypothèse nulle porte sur les deux facteurs ainsi que leur interaction. Il y a donc trois hypothèses à considérer et à tester. La première concerne l’effet simple de la variable SEXE (S)
H_{0 S} : X _S1 =  X _S2

La suivante, l’effet simple de la variable DOMAINE (D)
H_0 D : X_D1 =  X_D2 =  X_D3

La dernière concerne l’effet d’interaction entre les deux facteurs
H_{0 SxD} : X _S1xD1 =  X _S2xD1 =  X _S1xD2 = … =  X _SnxDn

L’hypothèse alternative (H₁) associée à chaque hypothèse nulle est qu’il existe une ou des différences de moyennes entre les groupes, c’est-à-dire qu’au moins une des moyennes est significativement différente des autres.

Prémisses du test d’ANOVA à plan factoriel

Les prémisses de l’ANOVA à plan factoriel sont les mêmes que celles de l’ANOVA :

1. Les groupes sont indépendants et tirés au hasard de leur population respective

Ceci signifie qu’il n’y a ni relation entre les observations à l’intérieur d’un groupe, ni relation entre les observations entre les groupes. Bien entendu, si on utilise un devis factoriel à mesures répétées ou mixte, cette prémisse ne doit pas être respectée lorsque l’on choisit comme 2^e variable catégorielle un temps de mesure.

2. Les valeurs des populations sont normalement distribuées

Nous avons vu comment estimer la normalité d’une distribution dans les sections précédentes. Cependant, l’ANOVA n’est pas très sensible aux écarts de la normalité. Il est donc possible de procéder sans avoir une normalité parfaite. Par contre, avec un petit échantillon, il faut faire attention à l’impact des valeurs extrêmes (on peut faire le test avec et sans les valeurs extrêmes).

3. Les variances des populations sont égales

Cette prémisse peut être vérifiée par l’examen visuel des graphiques boites à moustaches ou encore par le test de Levene qui est disponible dans les options de l’analyse. Si les groupes sont de tailles identiques, on peut passer outre cette prémisse. De plus, il est bon de mentionner que ce test est moins sensible aux variances qui ne sont pas égales que l’ANOVA.

Test de l’hypothèse nulle

Tout comme pour l’ANOVA, nous voulons déterminer si les différences de moyennes entre les groupes formés par les variables catégorielles sont issues de la variabilité naturelle ou si certains d’entres-eux se distinguent significativement de la moyenne populationnelle (H₁).

Nous travaillons avec le même ratio F que celui utilisé dans l’ANOVA et dans la régression linéaire. Nous devons donc répartir la variabilité totale en deux : la variabilité expliquée par le modèle (variabilité intergroupes, soit la variabilité entre les moyennes des groupes) et la variabilité résiduelle, soit celle qui n’est pas expliquée par le modèle (variabilité intra-groupe, c’est-à-dire la variabilité entre les individus autour de la moyenne de leur groupe).

Nous aurons toutefois 3 ratios F exprimant le rapport entre la variabilité expliquée par chaque composante du modèle (variable A, variable B, interaction AxB) et la variabilité résiduelle. Ces derniers seront interprétés dans la distribution F en fonction du degré de liberté de la composante et du degré de liberté résiduel.
Voyons un peu comment SPSS procède avec notre exemple d’analyse…  

La somme des carrés

Nous devons d’abord calculer la somme des carrés totale (SC_T) pour déterminer la variance à expliquer. Par la suite, cette variance peut être divisée entre celle qui est expliquée par le modèle (somme des carrés du modèle, SC_M) et celle qui ne l’est pas (somme des carrés résiduelle, SC_R).

Malheureusement, ça ne peut être si simple… les choses se corsent au moment de répartir SC_M en accordant à chaque VI la variance expliquée qui lui revient. Nous devons donc calculer la somme des carrés de la 1ère variable (SC_S), celle de la 2e (SC_D) et celle de leur interaction (SC_SxD).

1. La somme des carrés totale (SC_T)

C’est facile, nous utilisons la même équation que pour la régression simple, soit la variance de toutes les valeurs individuelles, sans tenir compte des variables indépendantes. La variance est calculée, comme vous le savez, en additionnant la différence mise au carré entre chaque score et la moyenne. Vous obtenez la dispersion des observations de la variable dépendante pour l’échantillon total, qui doit ensuite être divisée par N-1. Par contre, pour obtenir la somme des carrés, vous devez la  multiplier par N-1. Par conséquent, vous pouvez sauter les deux dernières opérations pour sauver du temps et utiliser directement la valeur de la dispersion. 

Le nombre de degrés de liberté (ddl_T) associé à la SC_T est N-1.

Voici la liste des du taux horaire initial des 44 participants. Le taux horaire moyen est de 26,13 $.

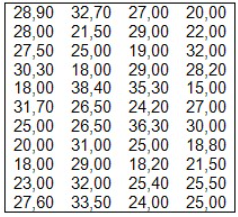
La variance est de 29,92. Nous devons multiplier cette somme par 43 pour obtenir la somme des carrés totale : 1286,56.

2. La somme des carrés du modèle (SC_M)

La SC_M ou la somme des carrés intergroupes représente la variabilité entre les groupes. Elle est calculée comme dans l’ANOVA en faisant la somme des différences entre la moyenne de chaque groupe et la  moyenne générale. Les différences sont multipliées par le N de chaque groupe. Il y a autant de groupes que de cellules dans le tableau créé par le croisement des deux VI. Dans notre cas, il est de 6 (2 catégories SEXE x 3 catégories DOMAINE).

Le nombre de degrés de liberté est égale au nombre de groupes (k) moins un.
Ce modèle permet d’expliquer 594,03 unités de variance de la variance totale à expliquer (1256,43 unités), avec un degré de liberté de 5.

2.1 L’effet principal de la 1ère VI (SEXE) (SC_S)
Nous devons séparer les salaires en fonction de l’appartenance au groupe, ce qui donne :

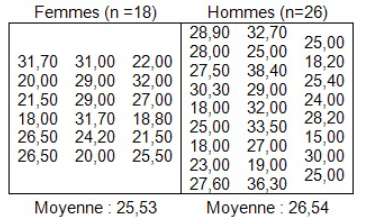
Le calcul de la SC_S donne une valeur de 10,85, avec un degré de liberté de 1.

2.2 L’effet principal de la 2e VI (DOMAINE) (SC_D)

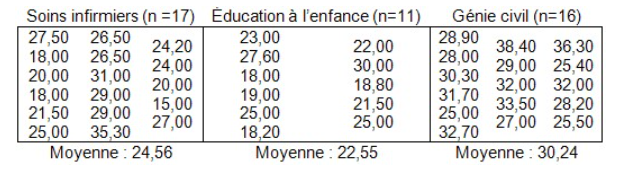
La SCD est de 453,15 et le degré de liberté, de 2. 

2.3 L’effet d’interaction (SC_SxD)

L’effet d’interaction se calcule plus facilement, puisqu’il représente la variance expliquée par le modèle une fois que l’on a retiré les effets des deux VI. L’équation est la suivante :

SC_SxD = SC_M – SC_S – SC_D = 130,03

Le nombre de degrés de liberté se calcule de la même façon :

ddl_SxDAxB = ddl_M – ddl_S – ddl_D.

Dans notre cas, il sera de 2.

3. La somme des carrés résiduelle (SC_R)

Comme dans l’ANOVA, la somme des carrés résiduelle ou la somme des carrés intra-groupe représente la variance individuelle dans les scores qui ne peut être expliquée par les variables introduites dans le modèle. Elle se calcule pour chaque groupe en multipliant la variance (écart-type au carré) par le nombre de sujets du groupe moins 1. 

SC_R = s²_groupe1 (n₁-1) + s²_groupe2 (n₂-1) + s²_groupe3 (n₃-1) + s²_groupe4 (n₄-1) + s²_groupe5 (n₅-1) + s²_groupe6 (n₆-1) = 675,14

Le degré de liberté sera cette fois la somme de tous les n-1, ce qui donne ddl_R = 37.

Les ratios F 

Ces derniers se calculent à partir des carrés moyens de chacune des sommes des carrés.

Vous pouvez ensuite calculer les mêmes ratios F que pour l’ANOVA

Une fois ces ratios F calculés, vous pouvez les comparer aux valeurs critiques dans la distribution F en fonction du nombre de degrés de liberté calculés. Dans notre cas, nous avons un numérateur de 1 pour le ratio F_S, mais de 2 pour les ratios F_D et F_SxD. Dans les deux cas, par contre, le dénominateur est de 37.

En regardant la distribution, nous constatons que pour p < 0,05 pour le ratio F_S, nous devons avoir une valeur de près de 4,08, ce qui n’est pas notre cas. Nous ne pouvons donc rejeter l’hypothèse nulle que ce ratio est différent de 0. Les hommes et les femmes obtiennent donc un salaire initial équivalent.

Par contre, pour F_D et F_SxD, la valeur doit respectivement être plus élevée que 3,23 pour que p < 0,05 et de 5,18 pour que p < 0,01. Nous pouvons donc rejeter l’hypothèse nulle pour ces deux ratios et dire que le domaine d’étude a un effet sur le salaire initial, tout comme l’interaction entre le domaine d’étude et le sexe. Bien évidemment, pour situer ces différences, il faudra avoir recours aux comparaisons post-hoc, qui sont expliquées dans l’avant-dernière partie du rappel théorique sur l’ANOVA.

La taille de l’effet

Du modèle factoriel : le tableau de résultats « Tests des effets inter-sujets » indique en note de bas de tableau une valeur R² qui correspond à la proportion de variance expliquée par le modèle factoriel. La valeur R² ajustée est plus conservatrice, car elle tient compte du nombre de facteurs insérés dans le modèle. C’est cette valeur qui devrait être utilisée lorsque différents modèles factoriels sont comparés.

Des facteurs : Le tableau de résultats « Tests des effets inter-sujets » fournit également le calcul de l’indice eta-carré partiel (η² partiel). Cet indice, comme toutes les mesures de la taille d’effet, doit être rapporté uniquement lorsque la valeur de F est significative. À la manière du R², la valeur eta-carré partiel indique la proportion de la variance spécifique expliquée par le facteur lorsque l’effet des autres facteurs est contrôlé. Comme ce dernier est basé sur la somme des carrés calculée à partir des valeurs de l’échantillon et n’est donc pas ajusté à la population, on peut lui préférer l’omega-carré (ω²). Cet indice de taille d’effet est toujours basé sur la somme des carrés, mais aussi sur la variance expliquée par le modèle et l’erreur de variance qui lui est associée. Vous pouvez trouver la procédure pour le calculer dans Howell (2002) ou dans Field (2005).

Le η² s’interprétera toujours de la même façon :