RAPPEL THÉORIQUE
Dans cette section, nous allons voir comment tester l’hypothèse nulle lorsque plus de deux moyennes sont confrontées. Le but sera toujours le même : vérifier l’hypothèse nulle que les moyennes des groupes proviennent d’une même population. Pour ce faire, nous allons utiliser l’analyse de variance univariée (ANOVA)
Cette technique permet de comparer les moyennes de trois groupes ou plus, créés par une variable catégorielle.
Hypothèse nulle
Les groupes proviennent de la même population. Leurs moyennes sont semblables.
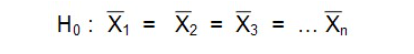
L’hypothèse alternative est qu’il y a une différence entre les moyennes, c’est-à-dire qu’au moins une des moyennes est différente des autres.
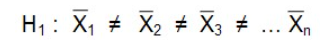
Prémisses du test d’analyse de variance
Tout comme pour les autres tests d’hypothèse, il faut s’assurer de respecter certaines prémisses avant de procéder à l’analyse proprement dite :
1. Les groupes sont indépendants et tirés au hasard de leur population respective
Ceci signifie qu’il n’y a ni relation entre les observations à l’intérieur d’un groupe, ni relation entre les observations entre les groupes. Par exemple, si on propose quatre traitements aux mêmes individus, il existe forcément une relation entre les observations et on ne pourra pas utiliser l’ANOVA dans ce contexte.
2. Les valeurs des populations sont normalement distribuées
Nous avons vu comment estimer la normalité d’une distribution dans les sections précédentes. Cependant, l’ANOVA n’est pas très sensible aux écarts de la normalité. Il est donc possible de procéder sans avoir une normalité parfaite. Par contre, avec un petit échantillon, il faut faire attention à l’impact des valeurs extrêmes (on peut faire le test avec et sans les valeurs extrêmes).
3. Les variances des populations sont égales
Cette prémisse peut être vérifiée par l’examen visuel du graphique boite à moustaches ou encore par le test de Levene qui est disponible dans les options de l’ANOVA. Si les groupes sont de tailles identiques, on peut passer outre cette prémisse.
Si la taille des groupes est très inégale, la prémisse d’égalité des variances doit être vérifiée systématiquement. Si le test est significatif, il est possible d’utiliser d’autres procédures disponibles dans le menu ANOVA : Test Brown-Forsythe ou le Welch Robust F.
Il est aussi possible d’utiliser les tests de comparaisons multiples qui ne demandent pas la prémisse d’égalité des variances.
Test de l’hypothèse nulle
Nous savons que même si la moyenne de la variable testée dans la population était la même pour les différents groupes formés par la variable catégorielle, nous n’aurions pas la même valeur de moyenne pour les différents échantillons puisque la moyenne d’un échantillon varie toujours. Des échantillons différents d’une même population produisent des moyennes et des écart-types différents.
Nous devons donc tester si ces différences sont attribuables à la variabilité naturelle de la moyenne entre différents échantillons d’une même population ou bien s’il y a une raison de croire qu’il existe un ou des groupes qui se distinguent réellement de la moyenne populationnelle.
Dans l’analyse de variance, nous allons diviser la variabilité en deux parties : la variabilité dans un groupe autour de la moyenne de chaque groupe, appelée variabilité intra-groupes (within-group) et la variabilité entre les moyennes des groupes, appelée variabilité inter-groupes (between-groups).
La statistique F produite par l’ANOVA est le rapport entre la variabilité inter et intra-groupes. Elle permet de déterminer s’il existe une différence significative entre les groupes. Comme la variabilité inter-groupes est le numérateur de ce rapport, plus les moyennes sont éloignées les unes des autres, plus la valeur F est élevée.
Tout comme la valeur t pour le test T, il faut comparer la valeur F obtenue à la distribution F. Le degré de signification va dépendre de trois facteurs : la valeur F et les deux degrés de liberté (inter et intra-groupes).
La distribution F
À l’image de la distribution normale et de la distribution t, la distribution F est calculée mathématiquement. Elle est utilisée lorsque l’on veut tester une hypothèse concernant la variance d’une population.
Le théorème central limite ne fonctionne pas avec la variance, la distribution des variances n’étant pas normale.
La distribution F représente le rapport entre les deux indices de variabilité et est indexée par deux degrés de liberté (inter et intra-groupes).
Comparaisons multiples
Le test d’analyse de variance ne nous dit qu’une chose : l’hypothèse nulle est rejetée ou non. Il ne nous dit pas où se situe la ou les différences. Il faut donc effectuer d’autres tests pour savoir entre quels groupes se trouve cette ou ces différences.
Ces tests sont appelés post-hoc ou tests a posteriori. Ils indiquent quels groupes se distinguent.
Pourquoi ne pas faire une série de tests t pour comparer chaque groupe entre eux ?
Parce qu’il y aurait plusieurs comparaisons pairées à effectuer ! Lorsque l’on effectue plusieurs tests de comparaisons sur les mêmes moyennes, on augmente les probabilités de trouver un résultat significatif uniquement par la chance même si les moyennes sont identiques dans la population. Ceci est ce qu’on appelle le problème des comparaisons multiples.
Pour y remédier, on utilise souvent une correction basée sur le nombre de comparaisons à effectuer. Plus il y a de comparaisons, plus le seuil de signification minimal devra être bas. Idéalement, on ne devrait observer que les comparaisons qui sont d’intérêt.
La correction de Bonferonni est l’une des plus simples, car elle ajuste le degré de signification en divisant 0,05 par le nombre de comparaisons à effectuer.
Au-delà de la signification statistique : la taille de l’effet
Tout comme pour les tests t, il est possible de calculer la taille de l’effet pour l’ANOVA. La formule est très simple puisqu’elle implique des éléments déjà calculés. Il faut toutefois savoir que le résultat représente la proportion de variance (R2) expliquée par le facteur (variable groupe ou variable indépendante).

En extrayant la racine carrée de ce rapport, on obtient la valeur de R (r) qui s’interprète de la manière suivante :
