RAPPEL THÉORIQUE
Dans cette section, nous allons voir comment tester l’hypothèse nulle à partir de deux moyennes provenant de deux échantillons (ou sous-groupes) indépendants. Nous allons en fait estimer si deux moyennes populationnelles sont égales en nous basant sur le résultat de la comparaison entre ces deux échantillons. La technique employée s’appelle Test t pour échantillons indépendants (Independent sample t test).
On utilise cette technique pour comparer DEUX groupes, créés par une variable catégorielle, en fonction de leur moyenne à une mesure (variable continue).
Hypothèse nulle
Il n’y a pas de différence entre les moyennes des deux groupes dans la population. En d’autres termes, la différence entre les deux moyennes dans la population est de 0. On sous-entend ici que les deux groupes proviennent de la même population.
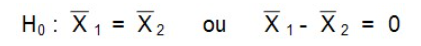
L’hypothèse alternative est qu’il y a une différence entre les deux moyennes.
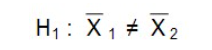
Prémisses du test t indépendant
Les données sont normalement distribuées.
La variable dépendante est continue.
Les variances des groupes sont égales (homogénéitéde la variance).
Les groupes sont indépendants (les mêmes observations ne peuvent pas être dans les deux groupes).
La différence de moyennes
Nous savons que même si la moyenne de la variable testée dans la population était la même pour les deux groupes formés par la variable catégorielle à deux niveaux, nous n’aurions pas la même valeur de moyenne pour les deux échantillons compte tenu du fait que la moyenne d’un échantillon varie toujours. Des échantillons différents d’une même population produisent des moyennes et des écart-types différents.
Pour déterminer si les différences entre les deux groupes reflètent une différence dans la population plutôt qu’une variation inhérente à l’échantillonnage, nous devons déterminer si les moyennes des deux groupes sont « inhabituelles » en faisant appel à la distribution échantillonnale des différences de moyennes.
Nous ne pouvons utiliser le test t pour échantillon unique, car nous avons à tenir compte de la variabilité non pas d’un, mais de deux groupes simultanément: la moyenne de chacun des sous-groupes.
Lorsque nous testons une seule moyenne en comparaison avec une moyenne populationnelle connue, nous n’avons pas à considérer comment les moyennes varient à l’intérieur de la population : cette variation est fixée par la théorie ou des études antérieures.
Le test t pour échantillons indépendants est une variation du test t pour échantillon unique qui incorpore l’information de la variabilité de deux moyennes provenant de deux échantillons indépendants.
L’erreur-type n’est plus estimée à partir de la variance et du nombre de sujets d’un seul groupe, mais bien des variances et des tailles des deux groupes indépendants.
Distribution échantillonnale des différences de moyennes
Dans le cas du test t pour échantillon unique, nous avons examiné la distribution échantillonnale de toutes les moyennes possibles provenant d’une population.
Nous avons ainsi vu que la variabilité échantillonnale des moyennes dépend de l’écart- type et de la taille de l’échantillon. La distribution des moyennes provenant de grands échantillons varie moins que celles provenant de petits échantillons.
De même, à taille d’échantillon égale, les moyennes provenant d’une population avec beaucoup de variabilité vont varier davantage que lorsqu’elles proviennent d’une population avec moins de variabilité.
Lorsqu’il est question de tester une hypothèse portant sur deux moyennes indépendantes, nous devons examiner la distribution de toutes les différences possibles entre les deux moyennes échantillonnales. Heureusement, le théorème central limite est valide avec les différences de moyennes échantillonnales aussi bien qu’avec les moyennes échantillonnales. Si les données proviennent d’échantillons d’une population approximativement normale ou si la taille de l’échantillon est suffisamment grande, la distribution des différences de moyennes entre deux échantillons est également approximativement normale.
Calcul de l’erreur-type de la différence de moyennes
Si nos deux groupes proviennent de deux populations avec la même moyenne, la moyenne de la distribution des différences est de 0. Cependant, il nous manque des informations pour déterminer si les résultats sont « inhabituels », car nous devons savoir dans quelle mesure les différences de moyennes varient parmi tous les échantillons possibles.
L’écart-type de la différence entre les moyennes de nos deux échantillons, soit l’erreur-type de la différence de moyennes, pourrait nous donner cette information. Avec deux groupes indépendants, nous devons estimer l’erreur-type de la différence de moyennes à partir de l’écart- type et de la taille de chaque groupe. En partant de l’hypothèse que les deux moyennes proviennent d’une même population, on peut calculer l’erreur-type de la différence de moyennes en utilisant la variance combinée (pooled variance).
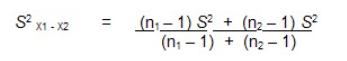
Calcul de la valeur de T
En connaissant maintenant l’erreur-type de la différence de moyennes, nous pouvons calculer la valeur de t de la même manière que lors des sections précédentes. Nous divisons la différence de moyennes observée par l’erreur-type de la différence.
Ce calcul nous indique à combien d’unités d’erreur-type se situe la différence observée de la moyenne populationnelle de 0.
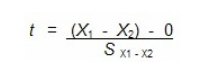
Interprétation du degré de signification
Lorsque le degré de signification est petit (p < 0,05), nous pouvons rejeter l’hypothèse nulle et conclure que les deux moyennes ne proviennent pas de la même population.
Cependant, il existe toujours une chance que cette conclusion soit fausse. Il est possible que l’hypothèse nulle soit vraie et que vos résultats soient parmi les possibilités peu probables. En fait, c’est ce que vous dit le degré de signification: quelle est la probabilité qu’une différence au moins aussi grande que celle observée apparaisse lorsque l’hypothèse nulle est vraie.
Lorsque le degré de signification est trop élevé (p > 0,05) pour rejeter l’hypothèse nulle que les moyennes sont égales, deux explications sont possibles :
a. Il n’y a vraiment pas de différence entre les deux moyennes (chose que vous ne pouvez pas prouver) ou il y a une petite différence que vous ne pouvez détecter;
b. Il y a une importante différence entre les deux groupes, mais vous ne l’avez pas détectée ! Comment cela est-il possible ? Une des raisons possibles est que l’échantillon est de petite taille et que plusieurs valeurs sont compatibles avec l’hypothèse nulle. Par conséquent, le résultat n’apparaît pas comme « inhabituel ». Par exemple, même s’il existait une grande différence entre les utilisateurs et les non utilisateurs d’Internet, avec 5 sujets dans chaque groupe, vous ne seriez pas en mesure de la détecter parce que la différence observée entre les deux groupes peut être compatible avec plusieurs valeurs de la population, dont la valeur 0.
La capacité de rejeter l’hypothèse nulle dépend aussi de la variabilité des valeurs observées. Si vous avez beaucoup de variabilité dans l’échantillon, l’étendue des valeurs possibles pour la vraie différence populationnelle sera grande.
Ces constats proviennent du fait que le calcul de l’erreur-type de la différence de moyenne repose d’une part sur la variance et, d’autre part, sur la taille de l’échantillon.
Au-delà de la signification statistique : la taille de l‘effet
Tout comme nous l’avions fait dans le cas du test t pour échantillon dépendant, il est possible d’aller apprécier l’importance ou la magnitude de la différence de moyennes entre les deux groupes grâce au calcul de l’indice eta-carré (η2).
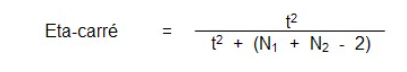
Les balises de Cohen (1988) sont les mêmes :
