Dans cet exemple, nous chercherons à identifier les variables qui permettent de prédire le plus efficacement la probabilité de vivre un épuisement professionnel chez les enseignants (ÉPUISEMENT). Nous vérifierons donc l’effet du stress généré par les élèves (ÉLÈVES), par les parents (PARENTS) et la direction (DIRECTION), le sentiment d’auto-contrôle (CONTRÔLE), les stratégies d’adaptation (ADAPTATION) et la présence d’un trouble anxieux (ANXIÉTÉ) sur la présence ou non d’un épuisement professionnel. Toutes les variables prédictrices évaluées sont continues, mise à part la variable anxiété qui est catégorielle. 

Étape 0 : le modèle de base

Le premier tableau indique simplement que SPSS a conservé les mêmes valeurs que celles utilisées pour coder les variables, soit 0 pour les individus qui ne sont pas épuisés et 1 pour ceux qui le sont.

Le tableau suivant illustre les valeurs utilisées pour la variable prédictrice catégorielle. Puisque nous avons choisi le contraste indicateur, nous conservons également les mêmes valeurs que pour coder la variable.

Le troisième tableau présente l’historique des itérations pour le modèle de base. Nous retenons particulièrement la probabilité log (-2LL) initiale. Elle est de 530,107 et représente la probabilité que nous chercherons à améliorer (réduire) en ajoutant des variables prédictrices.

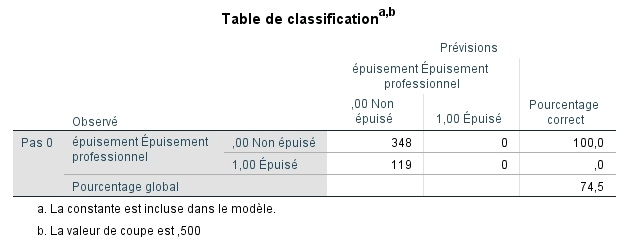
La table de classification montre pour sa part que la prédiction en se basant sur la catégorie la plus fréquente permet de classifier correctement 74,5 % des participants.

Le tableau des variables de l’équation nous indique la valeur du coefficient b₀. Dans notre cas, il est de – 1,073.

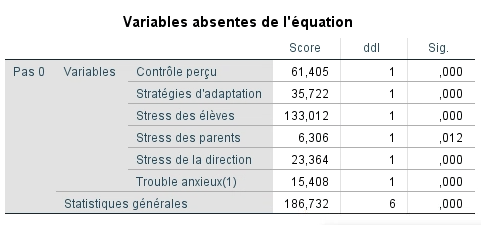
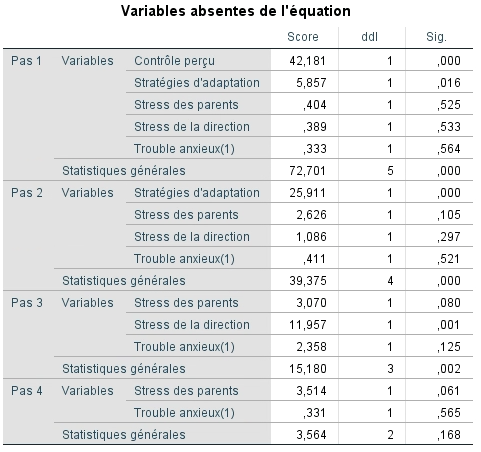
Enfin, le dernier tableau montre les valeurs de la statistique Score pour chaque variable prédictrice hors de l’équation qui s’apparente aux valeurs de corrélation partielle dans la régression multiple. Comme elles sont toutes significatives, elles contribueraient donc probablement toutes à l’amélioration du modèle.

Étape 1 : Évaluation de la signification du modèle de régression

Le tableau récapitulatif des modèles fournit les valeurs -2LL pour chaque étape du modèle. Nous pouvons déterminer si la probabilité – 2LL de chaque étape du modèle est inférieure à la probabilité – 2LL de base (530,11) et si cette différence est significative, ce qui nous indiquera si les termes de l’équation logistique finale prédisent mieux la probabilité de vivre un épuisement professionnel que ne le fait la probabilité initiale observée.

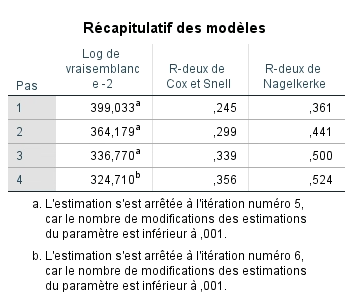
Par exemple, pour l’étape 1, nous pouvons calculer 530,11 – 399,033, ce qui donne 131,74. Cette valeur est évaluée dans une distribution χ² et sa signification est présentée dans le tableau tests de spécification du modèle. Nous constatons que l’étape (soit l’ajout de la variable adaptation) et le modèle complet sont significatifs. Bien sûr, à l’étape 1, le modèle ne comprend qu’une variable, donc nécessairement, la valeur χ² est identique pour les deux éléments. La ligne bloc ne sera examinée que dans une régression hiérarchique où on introduirait plus d’une variable (donc un bloc de variables) par étape.

Nous pouvons voir aux étapes suivantes que la ligne «étape» et la ligne «modèle» n’indiquent pas les mêmes valeurs. La ligne étape montre en effet la différence entre la probabilité -2LL de l’étape précédente et celle obtenue par l’ajout du nouveau prédicteur. Nous cherchons à ce qu’à chaque étape, le modèle présente une diminution significative du -2LL.

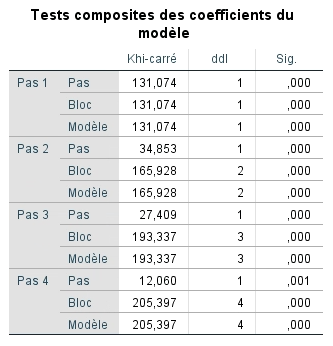
À la lumière de ces deux tableaux, nous pouvons dire que le modèle final permet de prédire significativement mieux la probabilité de vivre un épuisement professionnel que le fait le modèle incluant seulement la constante. 

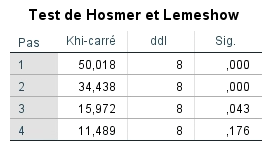
Nous pouvons ensuite examiner le test de Hosmer-Lemeshow. Celui-ci indique s’il existe un écart important entre les valeurs prédites et observées. Nous constatons à la lecture du tableau qu’il existe une différence significative entre les valeurs prédites et observées pour les étapes 1 à 3, mais que lorsque la 4^e variable est introduite, les valeurs prédites et observées sont cohérentes.

Étape 2 : Évaluation de l’ajustement des données au modèle de régression

Ensuite, il faut évaluer la signification statistique des coefficients estimés des variables indépendantes conservées afin de s’assurer que chacune contribue à mieux prédire P(y) qu’un modèle qui ne l’inclurait pas. Pour ce faire, nous nous basons sur la statistique Wald. Cette dernière illustre la différence dans le modèle avant et après l’ajout de la dernière variable. On observe qu’à l’étape finale, tous les coefficients sont significatifs, même si plusieurs variables ont été introduites. On rejette donc pour chaque variable que le coefficient est égal à 0. Par conséquent, chacune contribue à l’amélioration du modèle. 

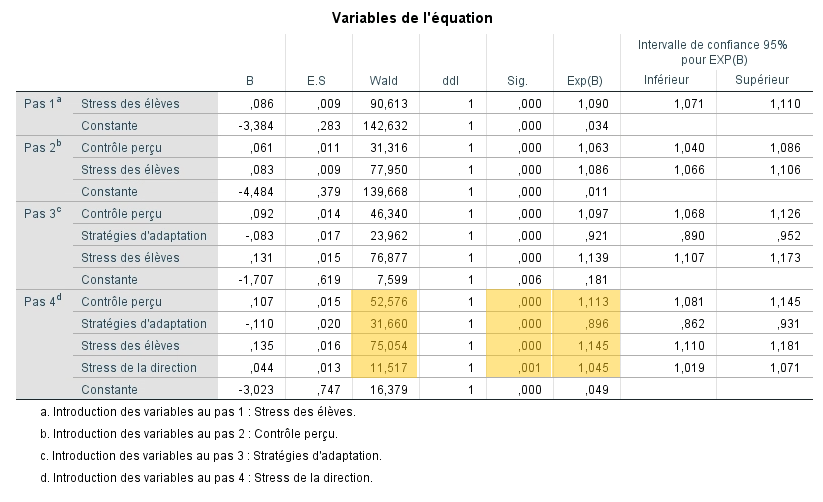
Le sens des coefficients b et de Exp(b) indiquent le sens de la relation. On constate donc que la relation est positive pour les variables contrôle, élèves et direction, soit que le faible sentiment de contrôle et le stress engendré par les élèves et la direction prédisent l’épuisement professionnel. Par contre, la relation est négative pour la variable adaptation, c’est donc dire que meilleures sont les stratégies d’adaptation de l’enseignant face au stress, moins il est probable qu’il vive un épuisement professionnel.

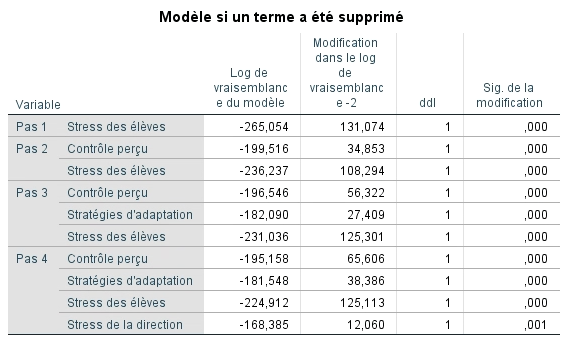
Le tableau suivant permet d’évaluer à chaque étape la présence d’un changement significatif de la probabilité -2LL lorsqu’une variable est retirée du modèle (la valeur doit être significative pour que la variable soit conservée).

Le tableau des variables hors de l’équation est aussi produit pour chacune des étapes. Comme lors du modèle initial, on peut observer que la ligne statistique globale est significative pour les étapes 1 à 3, donc que l’ajout d’une variable contribuerait à améliorer le modèle. À chaque étape, la variable qui a été incluse par SPSS est celle ayant la variable score la plus élevée dans la mesure où elle était significative.

Étape 3 : Évaluation de l’ajustement du modèle final

Nous savons maintenant que le modèle final est significatif et que chacune des variables indépendantes contribue significativement à mieux prédire P(y) qu’un modèle qui ne les inclut pas. Nous nous intéressons maintenant à savoir si le modèle est bien ajusté aux données. Pour ce faire, nous revenons au tableau récapitulatif du modèle pour voir les valeurs des R² de Cox et Snell et de Nalgelkerke. Comme le R² de la régression multiple, plus la valeur est élevée, mieux le modèle est ajusté aux données. Nous observons que la valeur augmente pour chaque étape et pouvons conclure que le modèle final est le mieux ajusté. 

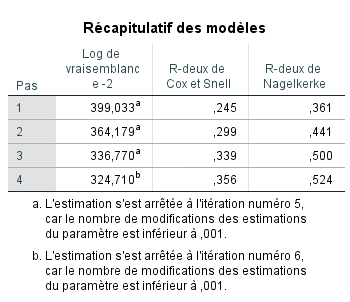
Il est également possible de calculer la valeur du Pseudo-R² pour obtenir un estimé de la variabilité expliqué.

0,39 = 530,107-324,710        

530,107

Le modèle final prédit donc 39 % de la variance de la probabilité de vivre un épuisement professionnel.

Étape 4 : Évaluation de la justesse de l’ajustement du modèle

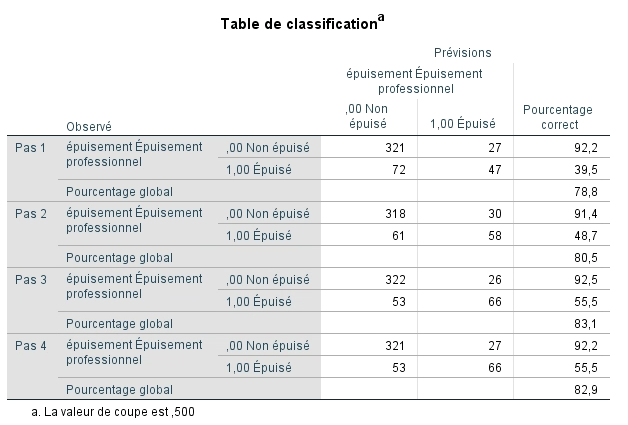
Il est maintenant possible d’examiner si le modèle permet de bien classer les sujets dans leur groupe d’appartenance à partir de l’équation finale. Nous nous rappelons que le hasard permettait de classer correctement 74,5 % des participants. Nous voyons que le pourcentage correct de classification passe de 78,8 % avec une seule variable indépendante et monte à 83,1 % pour l’étape 3. Il redescend minimalement à 82,9 % pour l’étape 4 où 92,2 % des enseignants non épuisés sont classés correctement, mais que seulement 55,5 % des épuisés le sont. Selon les résultats précédents, cette amélioration est significative.

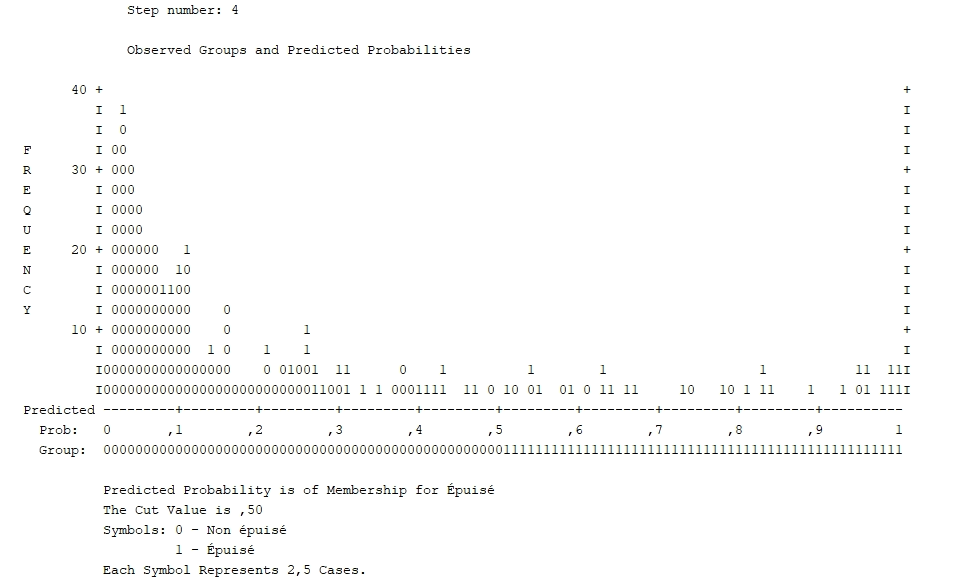
Le graphique des probabilités

Nous pouvons finalement examiner le graphique des probabilités. Il faut savoir que si le modèle était parfait, tous les participants épuisés (1) seraient situés vers la droite alors que tous ceux non épuisés (0) seraient vers la gauche. Idéalement, le moins d’individus possibles doivent être situés près du 0,5, puisque si plusieurs points sont près du centre, la probabilité est de 50/50, soit équivalente au hasard.

Nous constatons que la majorité des 0 sont à gauche, mais que la répartition des 1 est beaucoup plus étendue, ce qui nous confirme les résultats déjà analyses dans le tableau de classification.

Les résiduels

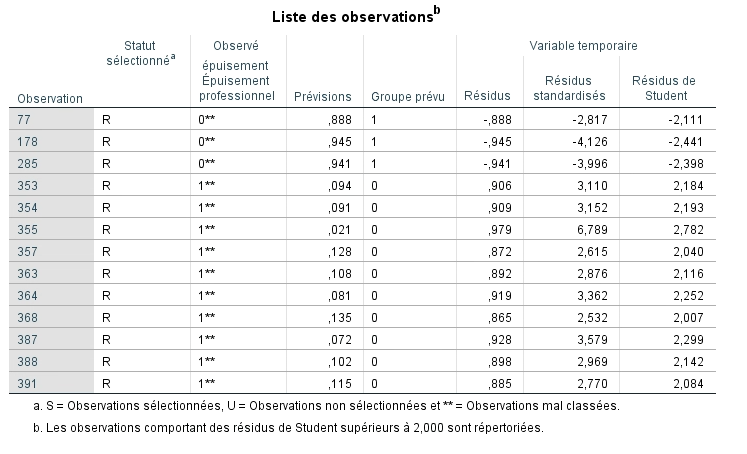
Finalement, on peut regarder le dernier tableau produit par SPSS, soit la liste des observations ayant une valeur résiduelle standardisée plus élevée que 2. Toujours dan l’optique de s’assurer que le modèle est bien ajusté aux données et qu’il prédit efficacement le groupe d’appartenance, nous conservons toujours les paramètres de la distribution normale, soit un maximum de

• 5 % des observations à l’extérieur des limites de ±1,96
• 1 % des observations à l’extérieur des limites de ±2,58
• et nous portons une attention particulière à celle situées à plus 3 écart-types.

Nous constatons que 7 observations sur le total de 467 participants ont des valeurs résiduelles de plus de 3 écarts-types, ce qui représente 1 % de l’échantillon. Il pourrait donc être intéressant de réaliser à nouveau l’analyse sans ces participants afin de vérifier si les coefficients estimés par le modèle varient beaucoup. Si c’était le cas, ces individus pourraient être considérés comme influençant l’ajustement du modèle.