Dans cet exemple, nous nous intéressons à la relation entre les groupes d’utilisateurs et de non-utilisateurs d’Internet (variable catégorielle à deux niveaux) sur le nombre d’heures passées à regarder la télévision (variable continue).

Statistiques descriptives

La première étape est un examen sommaire de la distribution de la variable testée en fonction des deux groupes, ceci dans le but de détecter la présence de valeurs extrêmes et de sélectionner le meilleur test d’hypothèse (technique). Voici les histogrammes pour la variable TVHOURS selon les groupes de sujets.

On remarque que chaque distribution a une queue vers les valeurs plus grandes signifiant que des sujets ont rapporté regarder la télévision plusieurs heures par jour.

Quelques-unes de ces valeurs nous font douter de la validité des réponses données. Par exemple, pour les non-utilisateurs, on observe certains sujets ayant donné 24 heures comme réponse. Nous savons que cela est impossible. Peut-être que certains répondants ont pensé que la question incluait le temps où la télévision était allumée sans qu’ils ne la regardent. On peut donc penser que cette variable, ou plutôt que la question formulée, n’est pas très précise. Cependant, nous allons considérer, pour les besoins de la cause, que les données représentent bien le nombre moyen d’heures passées à regarder la télévision.

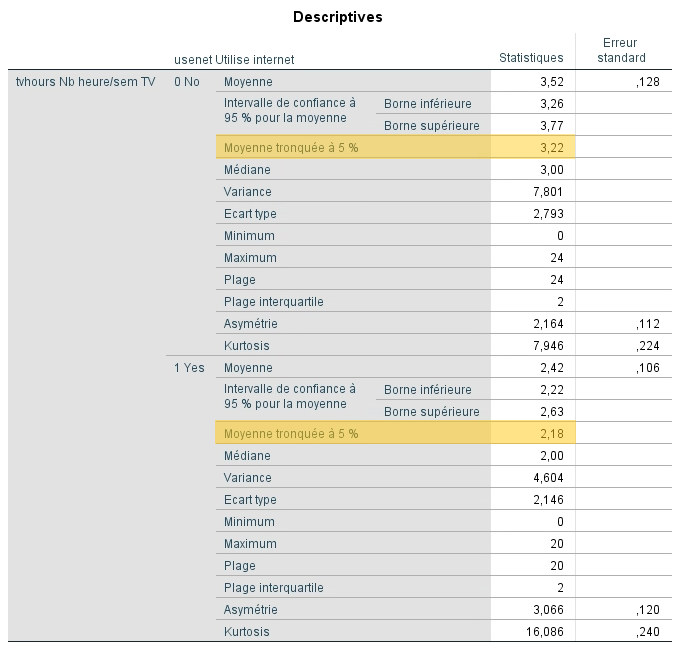
Le tableau Explorer, réalisé en mettant la variable USENET comme facteur, nous donne une idée de l’impact de ces valeurs extrêmes avec la moyenne tronquée qui est calculée en « coupant » 5 % des valeurs les plus basses et des valeurs les plus hautes. On remarque que le fait de ne pas considérer ces valeurs fait baisser les deux moyennes d’environ 0,3 heure.

Nous remarquons également que les non-utilisateurs d’Internet regardent la télévision en moyenne 1,1 heures de plus par semaine que les utilisateurs.

Nous devons déterminer quelles sont les probabilités d’observer une différence d’au moins 1,1 heures entre les deux groupes indépendants d’utilisateurs et de non-utilisateurs d’Internet si ces deux groupes proviennent de la même population (c’est notre hypothèse nulle). Pour ce faire, nous réalisons le test t pour échantillons indépendants.

Comme pour le test t pour moyennes dépendantes, le premier tableau montre un résumé des statistiques descriptives pour les deux groupes. Il indique le nombre de participants (N) ainsi que la moyenne et l’écart-type de chaque groupe pour le nombre d’heures passées à regarder la télévision chaque semaine. 

Dans la dernière colonne, SPSS affiche l’erreur standard moyenne, qui est, en fait, l’erreur-type.

Nous voyons encore une fois que les 473 non-utilisateurs d’Internet (x = 3,52) ont tendance à regarder en moyenne plus longtemps la télévision que les 413 utilisateurs (x = 2,42).

Résultat du test t

Le deuxième tableau contient les résultats du test. Il indique si la différence entre les moyennes des deux groupes est assez importante pour ne pas être due au hasard.

Les résultats montrent deux valeurs de t possibles. La première ligne de résultats concerne la situation où les variances des deux groupes sont égales (la différence entre les variance est de zéro) et la seconde ligne concerne la situation où les variances des deux groupes sont inégales. 

En fait, une des prémisses de l’utilisation du test t pour échantillons indépendants porte sur la nécessité de l’égalité des variances lors du calcul de l’erreur-type des différences de moyenne.

Le premier test effectué par SPSS est donc le test d’égalité des variances de Levene. Si ce test est significatif, on doit rejeter l’hypothèse nulle de l’égalité des variances et corriger le calcul de t en utilisant les variances individuelles des deux groupes (correction de Welch) plutôt que la variance combinée (pooled-variance). Voici la formule de l’erreur-type avec les variances individuelles :

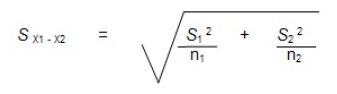
C’est ce calcul de l’erreur-type qui est utilisé dans la situation où le test de Levene est significatif. Cette correction dite de Welch implique notamment un calcul particulier du degré de liberté, mais cela va au-delà des objectifs de ce site.

Dans l’exemple, on voit que le test d’homogénéité des variances est significatif (p < 0,0005). Nous devons donc rejeter l’hypothèse nulle : les variances sont significativement différentes, la prémisse d’égalité n’est pas respectée. Nous devons donc lire la deuxième ligne. Dans le cas contraire, nous aurions interprété la première ligne.

Nous pouvons maintenant passer au résultat du test t proprement dit. On remarque que la valeur t, de la 2^e ligne est de plus de 6 et que le degré de signification est plus petit que 0,0005. On peut donc rejeter l’hypothèse nulle selon laquelle la différence de moyenne observée entre les deux groupes (1,1 heures) est compatible avec la différence populationnelle de 0. Il est donc très peu probable de trouver une différence de moyennes aussi grande lorsque les deux groupes sont considérés comme provenant de la même population. Le degré de signification indique qu’il est plus probable de postuler qu’ils proviennent plutôt de deux populations différentes.

La taille de l’effet

Nous savons maintenant que la différence observée entre les deux groupes n’est pas due au hasard. Il est possible de quantifier l’importance de cette différence à partir du calcul de l’indice eta-carré.

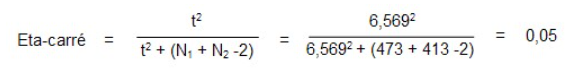
La valeur eta-carré indique la présence d’effet de moyenne taille pour le nombre d’heures passées à regarder la télévision (0,05).