Nous voulons savoir si les gens avec un diplôme collégial travaillent 40 heures par semaine. Nous allons donc comparer une moyenne d’un échantillon avec celle d’une population sans connaître l’écart-type de la distribution populationnelle.

Avec la base GSSNET, nous devons d’abord sélectionner les répondants ayant au moins un diplôme universitaire (DEGREE >= 3). Nous calculons ensuite le nombre d’heures moyen de travail par semaine.

Statistiques descriptives

Le premier tableau que nous fournit SPSS nous indique qu’il y avait 437 réponses valides pour cette variable. Le nombre d’heures travaillées en moyenne par les répondants est de 47,00.

L’histogramme réalisé à partir du menu Graphique montre que la distribution des heures a un pic plus élevé que celui d’une distribution normale (représentée par la ligne courbe) et que les queues sont assez allongées. Par contre, compte tenu de la taille de l’échantillon, on peut croire que la distribution échantillonnale de la moyenne sera normale.

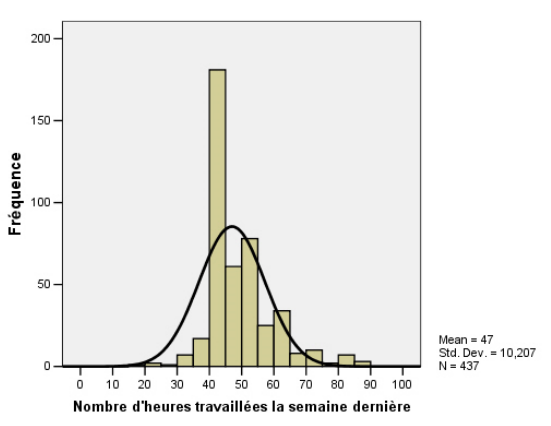
Donc, la moyenne de l’échantillon est de 47,00 heures par semaine. Nous voulons savoir si cette moyenne est « inhabituelle » par rapport à celle proposée pour la population. Nous devons donc positionner l’échantillon par rapport à la distribution échantillonnale de la moyenne. Comme nous ne connaissons pas l’écart-type de la population, nous allons positionner l’échantillon sur une distribution t.

Test-t sur échantillon unique

Le tableau suivant contient le résultat du test-t de moyenne pour un seul échantillon avec moyenne populationnelle connue. On remarque que la différence entre les deux moyennes apparaît dans le tableau sous la colonne Différence moyenne (5,170),  indiquant que la moyenne de l’échantillon est supérieure à celle de la population de 5,17 heures.

Ce tableau s’interprète ainsi: la probabilité d’observer un échantillon de cette taille ayant une moyenne de 47,00 si celui-ci est tiré d’une population ayant une moyenne de 40 est inférieure à 0,0005. Cet échantillon possède donc une moyenne extrêmement improbable dans l’hypothèse où il est tiré d’une population ayant une moyenne de 40 heures.

Le degré de signification est indiqué sous la colonne Sig. (bilatérale). Le fait de lire 0,000 ne signifie pas que la probabilité est nulle, mais qu’elle est plus petite que 0,005 (soit 0,05 %).

L’appellation bilatérale (2 queues) signifie que l’on prend en considération que le nombre d’heures aurait pu être plus grand ou plus petit que 40. Les deux alternatives sont possibles et intéressantes.

En se basant sur le degré de signification du score t, on peut dire qu’il est très improbable que les gens ayant au moins un diplôme collégial proviennent d’une population travaillant 40 heures par semaine. Les travailleurs semblent avoir un horaire hebdomadaire comprenant un nombre d’heures significativement plus élevé que celui généralement proposé.

Intervalle de confiance

Les deux dernières colonnes du tableau montrent que l’intervalle de confiance dans lequel la différence entre la moyenne de l’échantillon et la moyenne réelle de tous les travailleurs avec diplôme collégial se situe à 95 % entre 6,04 et 7,96.

On remarquera que la valeur 0 n’est pas incluse dans l’intervalle. Si c’était le cas, ceci voudrait dire qu’une différence nulle est une valeur possible. Nous devrions alors immédiatement conclure que les deux populations ne sont pas différentes (elles appartiennent à la même population).