RAPPEL THÉORIQUE
Nous avons vu au tout début comment examiner la distribution des proportions d’une variable catégorielle avec la procédure de fréquence. Maintenant, nous allons voir comment subdiviser les fréquences de proportion d’une variable catégorielle avec une autre variable catégorielle. Cette procédure s’appelle le tableau croisé.
Le tableau croisé examine la relation entre deux variables catégorielles. Il décrit donc la ventilation de chaque catégorie d’une variable en fonction d’une autre variable catégorielle.
Le tableau croisé est toujours formé de lignes et de colonnes. Tout comme dans une base de données, l’intersection d’une ligne et d’une colonne se nomme une « cellule ».
Pour illustrer cela, nous allons débuter avec la fréquence de distribution des valeurs de la variable catégorielle ordinale HAPPY qui mesure le degré de bonheur des gens. Les valeurs se trouvant à l’intérieur des cellules de ce tableau sont les effectifs réels.
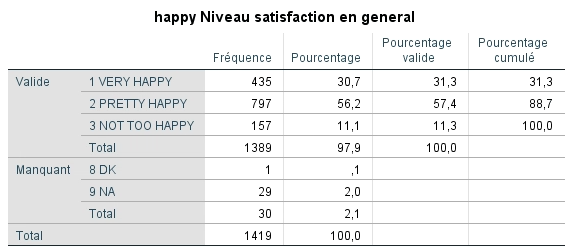
On remarque que 31 % des gens sont très heureux et que 11 % ne le sont pas tellement. Pour les conseillers en orientation, il serait très intéressant de connaître les caractéristiques des gens qui sont très heureux afin de mieux conseiller leurs clients pour qu’ils vivent une vie remplie de bonheur.
Tableau croisé contenant les occurences
Pour examiner la relation entre le degré de bonheur et, disons, le degré de scolarité, il faudrait prendre chaque ligne du tableau de fréquence (chaque catégorie) et la diviser sur la base des degrés de scolarité possibles dans la variable mesurée. Le tableau qui suit est un tableau croisé de la variable HAPPY et de la variable catégorielle ordinale DEGREE (degré de scolarité).

En lisant les lignes du tableau, on observe que les occurences initiales de la variable HAPPY ont été subdivisées en fonction du degré de scolarité des répondants. L’opération de ventilation (ou de croisement) consiste à identifier combien de répondants parmi la catégorie « Très heureux » ont moins qu’un secondaire cinq (valeur « 0 » de DEGREE), soit n = 58, combien ont un diplôme d’études secondaires (valeur « 1 » de DEGREE), soit n = 211 et ainsi de suite. SPSS fait la même opération pour les autres catégories de HAPPY.
Le total lu en ligne nous donne le nombre total d’observations (effectifs) ayant comme valeur « 1 », « 2 » et « 3 » dans la base de données à la variable HAPPY. On remarque que les valeurs totales pour HAPPY dans le tableau croisé sont exactement les mêmes que dans le tableau de fréquences de départ.
Le total lu en colonne donne le nombre total d’observations ayant comme valeur « 0 », « 1 », « 2 », « 3 » et « 4 » dans la base de données pour la variable DEGREE.
Tableau croisé contenant les pourcentages (%)
Un tableau croisé dans lequel les cellules contiennent le nombre de cas ne permet pas de tirer des constats sur la relation entre les deux variables, puisque le nombre de personnes dans chaque niveau de scolarité varie énormément.
Pour parvenir à comparer les cellules entre elles, il faut préalablement calculer les proportions de gens dans chaque cellule. Ces proportions peuvent être en colonne ou en ligne. Nous verrons dans la section Procédure SPSS comment insérer les pourcentages dans les cellules.
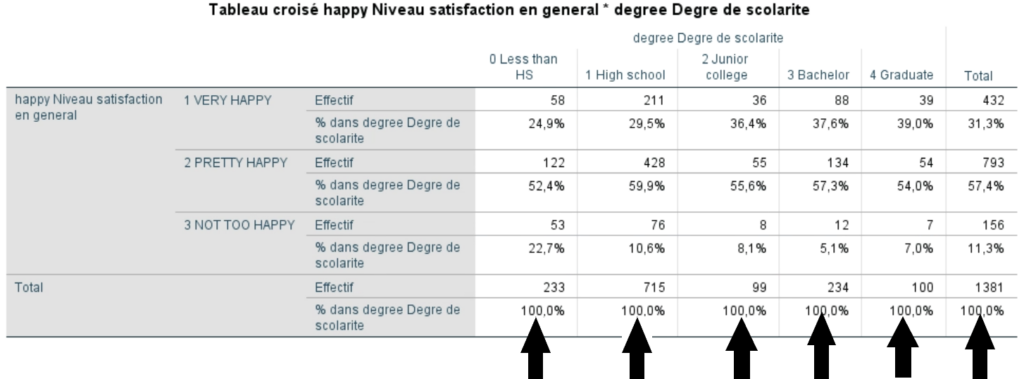
Comment faire pour distinguer si les pourcentages sont en colonne ou en ligne?
Il suffit simplement de regarder la dernière ligne et la dernière colonne où se situent les totaux du tableau croisé. Si la dernière ligne contient les totaux en pourcentage (100 %), c’est que les pourcentages ont été calculés en colonne. L’inverse s’applique si les totaux à 100 % se trouvent dans la dernière colonne. Dans ce cas, les pourcentages ont été demandés en ligne.
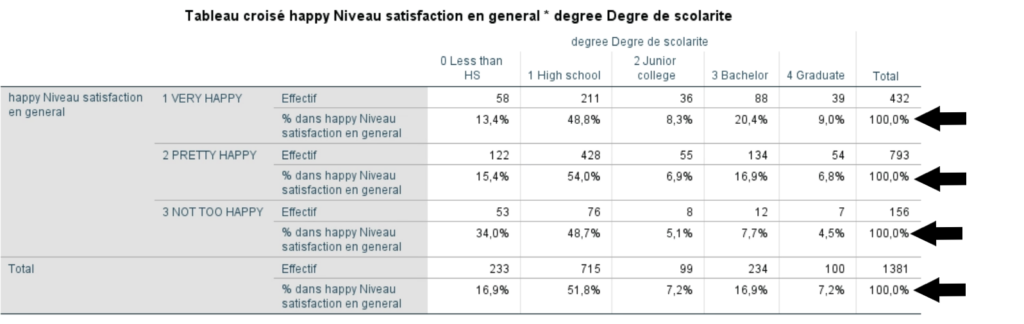
Comment déterminer quel type de pourcentage est pertinent ?
Il faut déterminer quelle information est recherchée au départ. Pour ce faire, on peut penser en termes de variable dépendante et de variable indépendante. Dans les analyses bivariées, la variable indépendante est celle qui théoriquement influence l’autre variable, la variable dépendante. Elle représente également souvent un attribut relativement fixe (ex. : caractéristiques socio-démographiques).
Par exemple, dans une étude portant sur l’impact de la cigarette sur le cancer du poumon, le fait de fumer ou non est la variable indépendante, car on prétend que le fait de fumer influence directement l’apparition du cancer du poumon. Dans la relation entre le sexe et la catégorie de revenu, le sexe est la variable indépendante, car il est souvent déterminant (malheureusement) de l’échelle salariale.
Si vous êtes en mesure d’identifier la variable indépendante dans la construction de votre tableau croisé, alors vous devriez configurer votre tableau pour que les totaux de 100 % soient au bout de chaque catégorie de la variable indépendante.
Dans l’exemple précédant, la variable indépendante est … le niveau de scolarité atteint. Alors, la bonne façon de construire le tableau est celle des pourcentages en colonne où chaque catégorie de scolarité avait effectivement un total de 100 %.