Dans notre exemple, nous voulions savoir si les hommes et les femmes (variable indépendante SEXE) en soins infirmiers, en éducation à l’enfance et en génie civil (variable indépendante DOMAINE) gagnent en moyenne le même salaire horaire après avoir reçu leur diplôme collégial (variable dépendante SALAIRE).

La question à laquelle nous allons répondre est donc : Est-ce que le salaire initial moyen varie chez les diplômés du collégial en fonction du sexe et du domaine d’études ?

Nous allons tester trois hypothèses :

1. Il n’y a pas de différence entre le salaire horaire moyen des hommes et des femmes à la sortie du collégial (tout domaine confondu).

2. Il n’y a pas de différence entre le salaire horaire moyen des infirmiers, des éducateurs et des techniciens en génie civil à la sortie du collégial (tout sexe confondu).

3. Il n’y a pas de différence de salaire horaire moyen en fonction du sexe ET du domaine d’études.
 

Statistiques descriptives

Le premier tableau fournit par SPSS nous indique combien de participants forment notre échantillon. Nous voyons que notre échantillon est divisé selon les deux facteurs. Une première fois en fonction du sexe (18 femmes et 26 hommes) et une seconde fois en fonction du domaine d’études (17 diplômés en soins infirmiers, 11 en éducation à l’enfance et 16 en génie civil).

Nous observons ensuite les moyennes obtenues pour chacun des 6 sous-groupes formés par le croisement des deux variables indépendantes.

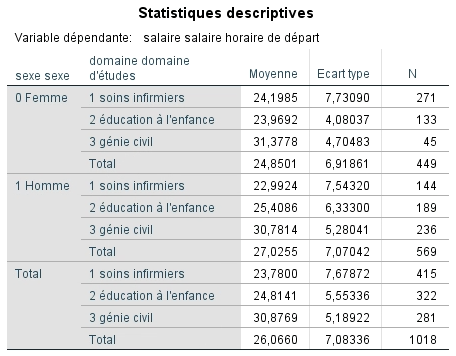
Nous observons que les femmes gagnent en moyenne 24,85 $ de l’heure alors que les hommes gagnent 27,03 $ de l’heure. Du côté des domaines d’études, les éducateurs gagnent le salaire le plus faible, soit 24,81 $, suivis des infirmiers et infirmières avec 23,78 $. Les techniciens en génie civil gagnent un salaire plus élevé (30,88 $) que les deux autres groupes. Nous observons la même tendance en fonction du diplôme chez les femmes. Par contre, les hommes éducateurs gagnent un salaire plus élevé (25,41 $) que les infirmiers (22,99 $).

À première vue, il semble exister des différences en fonction du sexe et du domaine d’études, mais est-ce que ces différences sont simplement dues à la variabilité naturelle ou est-il possible de croire que ces différences sont suffisamment importantes dans la population pour que l’on puisse rejeter l’hypothèse nulle voulant que tous les diplômés peu importe leur domaine d’études et leur sexe gagnent un salaire initial équivalent ?
 

Homogénéité des variances

Même si nous savons que l’analyse de variance à plan factoriel est moins sensible à l’inégalité des variances, nous jetons tout de même un coup d’œil.

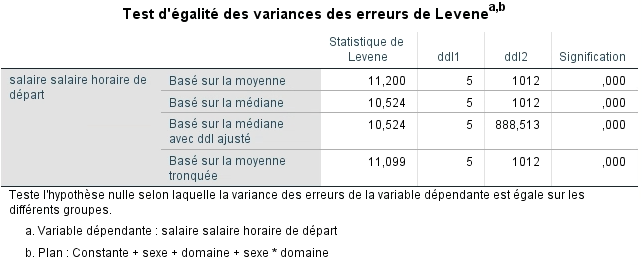
Nous voyons d’abord la statistique proprement dite, puis les degrés de libertés selon lesquels elle est interprétée : le premier est le nombre de groupes moins 1 (k -1) et le second, le nombre de participants moins le nombre de groupes (N-k). Dans la dernière colonne, nous constatons que le test n’est pas significatif, ce qui signifie que nous pouvons conserver H0 et dire que dans notre échantillon, les variances des sous-groupes sont équivalentes.
 

Résultats de l’analyse principale

Les éléments importants à observer dans le tableau sont, pour chacune des variables et du terme d’interaction, les valeurs F et leurs significations. Ces dernières nous permettront de répondre à notre question de recherche.

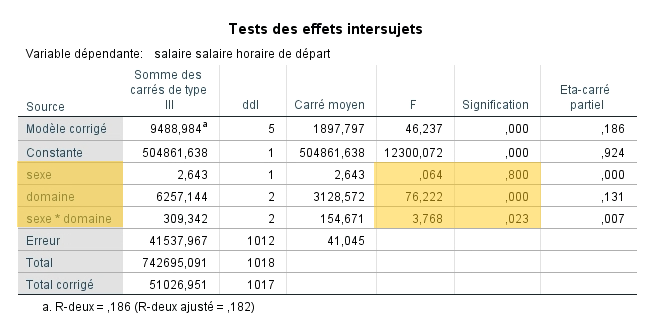
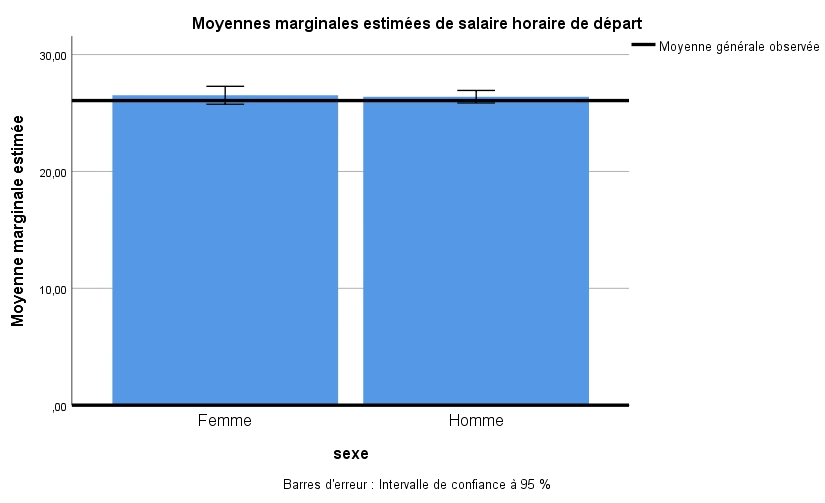
Effet du facteur SEXE : Nous constatons d’abord que la valeur F de la variable sexe n’est pas significative (F(1,42)=0,02, n.s.). Nous ne pouvons donc pas rejeter H₀ et nous devons conclure que les hommes (X = 27,03 $) et les femmes (X = 24,85 $) gagnent un salaire moyen équivalent à leur sortie du collégial lorsque nous ne tenons pas compte du domaine d’études. Nous pouvons d’ailleurs illustrer cette absence de différences par le graphique à barres ci-dessous. L’option Afficher les barres d’erreurs-Intervalles de confiance a été sélectionnée). Nous voyons que les deux barres sont sensiblement à la même hauteur.

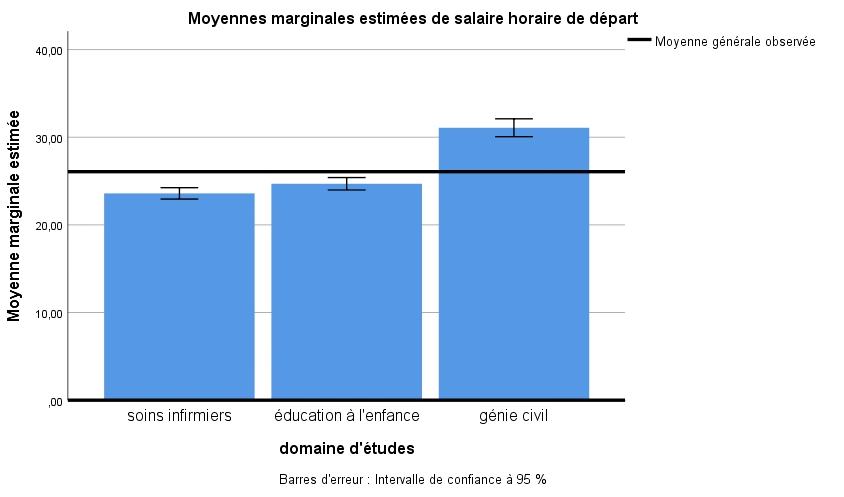
Effet du facteur DOMAINE : En revenant au tableau d’analyse principale, nous constatons que contrairement à la valeur F de la première variable, celle associée à la variable domaine est significative (F(2,41) = 9,91, p < 0,001). Nous pouvons rejeter H₀ pour cette variable, car il est très peu probable (moins de 0,1 % de chances) que dans la population, les finissants des trois domaines comparés gagnent le même salaire à la fin de leurs études lorsque nous ne tenons pas compte de leur sexe. Encore une fois, nous pouvons utiliser le graphique pour mieux visualiser les données. Nous voyons bien que les bâtons se situent à des niveaux différents. Nous pouvons même supposer qu’il existe un écart plus important entre les diplômés en technique de génie civil et en éducation à l’enfance qu’entre les autres groupes, mais nous devons attendre d’examiner le tableau de comparaisons multiples pour nous en assurer.

Effet du facteur d’interaction SEXE x DOMAINE : Finalement, nous pouvons regarder la valeur F associée à l’effet d’interaction. Cette dernière est significative (F(1,39)= 3,66; p = 0,04). Cela signifie que l’effet du domaine d’études sur le salaire varie en fonction du sexe du finissant. Malheureusement, SPSS ne produit pas de tableau nous indiquant où se situent ces différences. Nous pouvons toutefois observer le graphique des moyennes marginales estimées qui illustre l’effet d’interaction.

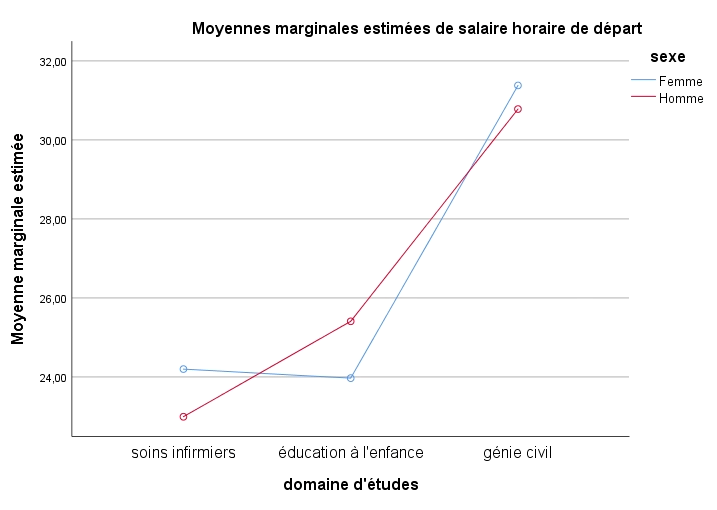
Nous constatons que chez les femmes, les différences de salaire sont plus importantes entre les éducatrices et les techniciennes en génie civil.  Celles-ci gagnent un salaire qui se rapproche davantage de celui des infirmières. Chez les hommes par contre, nous voyons que les infirmiers et les éducateurs gagnent un salaire initial plutôt similaire, mais qu’il existe une différence importante entre ces deux groupes et les techniciens en génie civil. La variation dans les salaires des hommes et des femmes confirme l’effet principal du domaine d’études sur le salaire.

Le croisement entre la ligne des hommes et celle des femmes confirme l’effet d’interaction entre les deux variables. Ce graphique semble illustrer que les infirmières gagnent plus que les infirmiers, mais que les éducateurs ont un salaire plus élevé que les éducatrices. Nous pouvons voir que la différence de salaire entre les hommes et les femmes ne semble vraie que pour les deux premiers domaines d’études : on ne voit qu’un très faible écart entre le salaire des finissants et des finissantes en technique de génie civil.

Contrastes

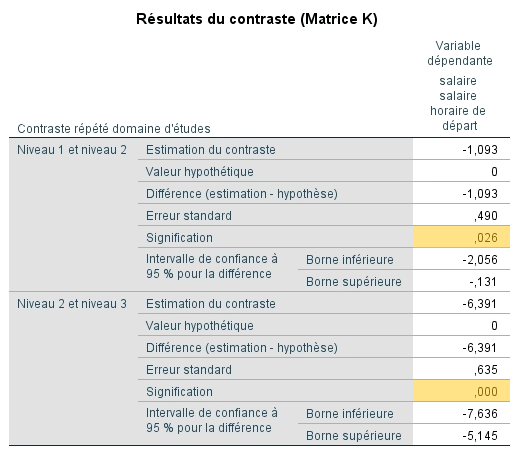
Si nous voulons confirmer ces observations, nous pouvons regarder où se situent les différences significatives pour le domaine d’études dans le tableau des contrastes. Nous voyons que la différence entre le niveau 1 (soins infirmiers) et le niveau 2 (éducation à l’enfance) n’est pas significative, contrairement à celle entre le niveau 2 et le niveau 3 (génie civil). Ces résultats confirment l’hypothèse émise en regardant le graphique à barres : il existe une différence significative entre le groupe éducation à l’enfance et génie civil à l’effet que ces derniers gagnent plus que les premiers, mais il n’y a pas de différence entre les deux autres groupes. Nous ne savons toutefois pas s’il existe une différence entre le niveau 1 et le niveau 3. Nous pourrions refaire une analyse de contraste simple, mais nous allons plutôt regarder les résultats des analyses post-hoc.

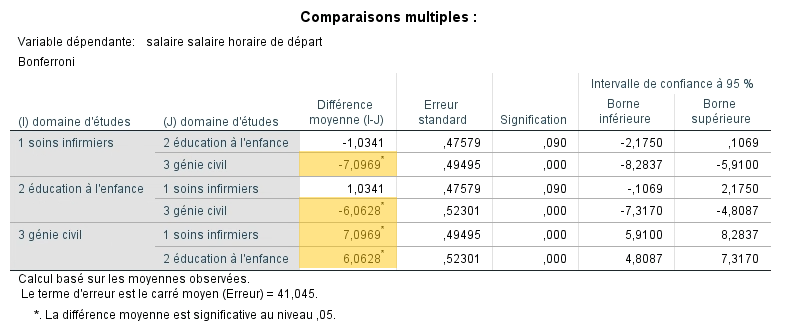
Analyses post-hoc

Pour terminer, le tableau des comparaisons multiples confirme les résultats précédents : une différence significative existe entre le salaire des éducateurs et des techniciens en génie civil. SPSS révèle qu’une différence significative est également observable entre le 3e groupe et les infirmiers et infirmières. Il semble donc que les finissants en technique de génie civil obtiennent un salaire supérieur à celui obtenu par les deux autres groupes qui eux, ne se distinguent pas.

Taille d’effet

Finalement, en ce qui concerne la taille d’effet, nous pouvons regarder l’eta-carré partiel (η² partiel) fournit par SPSS dans le tableau d’analyse principale pour les deux effets significatifs (DOMAINE = 0,34; SEXE*DOMAINE = 0,16). Si on se fie aux balises de Cohen (1988), dans le premier cas, l’effet est de grande taille, mais dans le second, il est de taille moyenne.