RAPPEL THÉORIQUE
Tout comme l’ANOVA, la procédure ANCOVA vise à déterminer l’effet d’une variable catégorielle (indépendante) sur une variable continue (dépendante).
La particularité de l’ANCOVA est de calculer cet effet en contrôlant l’effet d’une autre variable continue qui a un impact présumé sur la relation initiale.
Par exemple, pour comparer les temps de course de trois groupes en boîte à savons, le poids des coureurs a certainement une influence qu’il faudrait contrôler. Cette variable contrôlée est appelée « covariable ».
La covariable est nommée ainsi, car on la suspecte de covarier avec la variable dépendante et d’affecter indirectement la relation qui existe entre la variable indépendante et la variable dépendante.
Le but de l’ANCOVA est de tester la relation initiale en supprimant statistiquement l’effet indirect de la covariable. Ceci revient à tester l’effet de la variable indépendante (catégorielle) sur la variable dépendante (continue) une fois que l’effet de la covariable sur la variable dépendante est enlevé.
Hypothèse nulle
Dans l’ANCOVA, nous testons l’hypothèse nulle de l’absence de différence entre les moyennes des groupes une fois que l’effet de la covariable est retiré.
L’hypothèse alternative est donc que les moyennes des groupes se distinguent.
Prémisses de l’ANCOVA
Les trois première prémisses sont les mêmes que pour l’ANOVA :
1. Les groupes sont indépendants et tirés au hasard de leur population respective
2. Les valeurs des populations sont normalement distribuées
3. Les variances des populations sont égales
Nous devons toutefois respecter une quatrième condition avant de procéder à l’ANCOVA :
4. Les droites de régressions sont homogènes
Nous devons en effet regarder la relation entre la variable dépendante et la covariable. Pour comprendre cette prémisse, imaginons que nous réalisons un nuage de points avec la covariable et les valeurs de la variable dépendante pour chacun des groupes créés par la variable catégorielle. S’il existe une relation linéaire positive entre la variable dépendante pour un groupe et la covariable, nous espérons que la relation ira dans le même sens pour les autres groupes. Vous pouvez tester cette prémisse à partir du bouton Model de la boîte de dialogue principale de l’ANCOVA.
Qu’est-ce que la covariance
La covariance est une mesure de l’association ou du lien qui existe entre deux variables. Pour comprendre la covariance, revenons à la notion de variance. La variance d’une variable est une mesure qui quantifie la dispersion moyenne des valeurs prises par cette variable autour de sa moyenne. On se souvient de la formule pour quantifier cette dispersion.
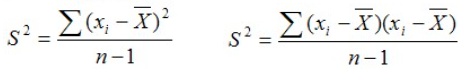
Deux variables covarient ensemble lorsqu’un écart à la moyenne d’une variable est accompagné par un écart dans le même sens ou dans le sens opposé de l’autre pour le même sujet. Plus ce pattern est présent dans l’ensemble des observations, plus les deux variables semblent partager une association entre elles. Autrement dit, deux variables covarient lorsque la variation d’une des variables autour de sa moyenne semble influencer la manière dont l’autre variable varie autour de sa moyenne. La covariance exprime donc une quantité de variance partagée entre deux variables. En effet, tout comme la variance, la covariance peut se quantifier. Plus la valeur de la covariance est élevée, plus les deux variables partagent une portion importante de variance. Voici la formule permettant de calculer la covariance entre deux variables continues.
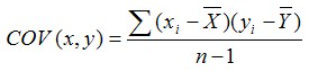
L’examen du produit des parenthèses nous indiquent ceci : lorsque les valeurs de x et y sont du même côté de leur moyenne respective, le produit des parenthèses (la valeur de l’élément de sommation) sera positif. Inversement, si les valeurs pairées de x et y ne sont pas du même côté de leur moyenne respective, le produit des parenthèses (la valeur de l’élément de sommation) sera négatif. Si la valeur totale de la sommation est positive, ceci représente la tendance d’un grand nombre de valeurs x et y à varier dans le même sens autour de la moyenne: si x est au-dessus de sa moyenne, y l’est aussi. Si la valeur totale de la sommation est négative, c’est que pour une bonne partie des observations, les valeurs pairées x et y se retrouvent à des endroits opposés de leur moyenne respective : si x est au-dessus de sa moyenne, y est en-dessous (et vice-versa). Pour illustrer ceci, voici un exemple simple.

Cinq sujets ont été suivis pendant une semaine. On a compté le nombre de boissons Coke bues par chaque personne et le nombre de publicités de cette compagnie auxquels ils ont été exposés.
Le tableau de données montre les valeurs de chaque variable pour les cinq sujets ainsi que la valeur des moyennes.
Le graphique montre la dispersion de ces valeurs autour de la moyenne de chaque variable.
On remarque que pour les cinq sujets, les variations autour de la moyenne de la variable V1 sont accompagnées par un mouvement qui va dans la même direction pour la variable V2 (et inversement).
Dans le calcul de la covariance, on obtient un indice qui est le produit des deux variances des variables en jeu et ce produit varie toujours selon les échelles utilisées. Si nous appliquons la formule pour calculer la valeur de la covariance entre ces deux variables, nous obtenons :
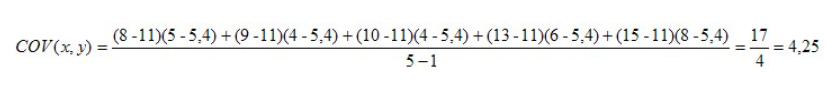
La valeur 4,25 est positive, ce qui signifie que les paires de valeurs x et y varient dans le même sens autour de leur moyenne respective. Le graphique montre bien cette variation similaire entre les deux variables. Cette façon de décrire la relation entre les deux variables devrait vous rappeler le contenu du chapitre portant sur le croisement entre deux variables continues dans la section sur les statistiques descriptives (graphique nuage de points). En effet, le calcul de la covariance est directement relié à l’estimation de la relation linéaire entre deux variables continues. Si la covariance est positive, la relation linéaire entre les variables est également positive et si la valeur de la covariance est négative, la relation linéaire entre les deux variables est aussi négative.
Ultimement, l’estimation de la force et du sens de la relation entre deux variables est calculée à l’aide du coefficient de corrélation. Ce coefficient est simplement une standardisation de la covariance. Voici la formule du coefficient de corrélation de Pearson basée sur la covariance.
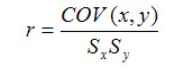
La procédure ANCOVA
La procédure ANCOVA est utile lorsque le chercheur croit que l’effet d’une troisième variable (continue) vient brouiller la relation entre la variable catégorielle et la variable continue de l’ANOVA.
On applique aussi régulièrement cette procédure dans les études quasi-expérimentales avec des mesures pré-test et post-test. On se sert de la mesure pré-test comme covariable pour annuler les différences de performances entre les groupes avant l’intervention. Ainsi, les différences observées au post-test seront dénuées des variations de la mesure au pré-test.
La taille d’effet
Dans les options de l’ANCOVA, il est possible de demander l’indice eta-carré (η2) qui permet d’apprécier l’importance de l’effet de la variable indépendante sur la variable dépendante. Les balises de Cohen (1988), pour ce test, sont les suivantes :
