1.    Contrairement aux autres tests de statistiques inférentielles, le test de Chi-2 se trouve dans le menu Statistiques Descriptives – Tableaux croisés. Eh oui! C’est le même chemin que pour faire un tableau croisé, pour la simple raison que la statistique du Chi-2 est calculée à partir du tableau croisé !

2.     Dans la boite principale, vous insérez la variable en rangée dans la boite Ligne(s) et l’autre dans la boite Colonne(s).

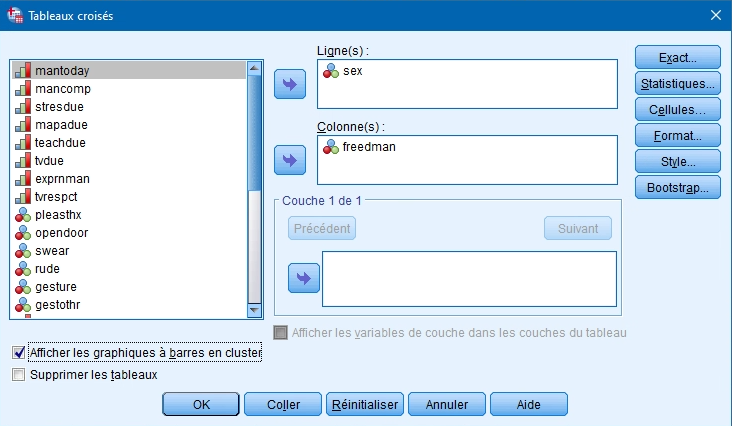
3.     Dans le bas de la boite principale, vous indiquez si vous désirez obtenir le graphique à barres (Afficher les diagrammes en bâtons juxtaposés) qui illustrera les fréquences observées. 

4.    Si vous cochez Supprimer les tableaux, vous obtiendrez seulement un tableau présentant le nombre de réponses valides et le graphique à barres.

5.      Vous cliquez ensuite sur la flèche.

Tableau croisé en strates : ajout d’une variable contrôle

Pour ce faire, vous devez ajouter la ou les variables contrôles, qui seront aussi placées en colonne, dans la boite Couche. Si vous insérez plus d’une variable contrôle, vous devez appuyer sur le bouton SUIVANT avant d’ajouter la deuxième variable.

Le bouton EXACT

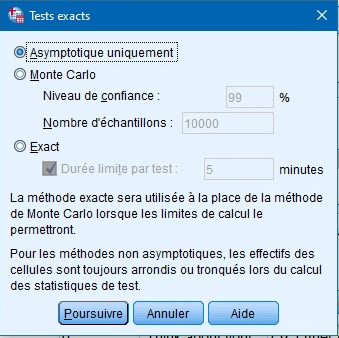
Cette option vous permet de choisir si vous désirez que les calculs soient faits à partir des nombres arrondis ou des nombres exacts.

Le bouton STATISTIQUES

Ce bouton vous permet de choisir le type de test que vous désirez utiliser pour évaluer s’il y a une association significative entre les variables.

Dans notre cas, nous choisissons le test de Khi-carré plutôt que le test de corrélations. Ce dernier est habituellement utilisé pour évaluer s’il existe une relation entre des variables continues, mais il est également possible de calculer un coefficient de corrélation entre deux variables catégorielles dans certains contextes. 

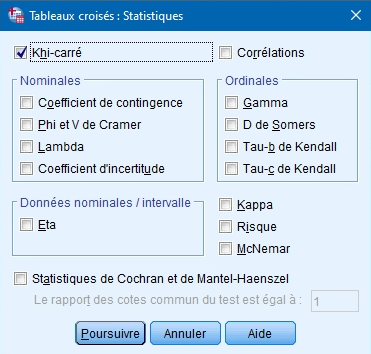
L’encadré Nominales vous offre différents tests pour apprécier la force de l’association évaluée par le Chi-2 pour des variables catégorielles nominales.

• Coefficient de contingence : cette mesure est basée sur le Chi-2. Sa valeur oscille entre 0 et 1, mais puisqu’elle atteint rarement son maximum, le V de Cramer lui est préféré.
• Phi et V de Cramer : ces deux mesures sont aussi basées sur le Chi-2, mais elles ajustent la statistique en fonction de la taille de l’échantillon et des degrés de liberté. Le V de Cramer est  le plus utilisé.
• Lambda : ce test reflète la proportion de la réduction de l’erreur associée au modèle lorsque la valeur de la variable indépendante est utilisée pour prédire la variable dépendante. Lorsque la valeur est 1, la variable indépendante prédit parfaitement la variable dépendante. Lorsque la valeur est 0, la variable indépendante ne permet pas de prédire la variable dépendante.
• Le coefficient d’incertitude : cette mesure d’association indique la proportion de la réduction de l’erreur associée au modèle lorsqu’une variable est utilisée pour en prédire une autre.

Dans notre cas, nous choisissons le Phi et le V de Cramer.

Vous l’aurez deviné, l’encadré Ordinales offre des tests similaires à ceux proposés dans l’encadré Nominales, mais ces tests sont utilisés lorsque le Chi-2 évalue l’association entre différentes variables catégorielles ordinales. La mesure la plus utilisée est le Gamma. Sa valeur varie entre – 1 et 1. Les valeurs près de 0 indiquent une relation faible ou inexistante.

L’encadré Données nominales x intervalle propose l’indice eta-carré qui ne peut être utilisé que si l’on croise une variable catégorielle avec une variable continue.

Kappa : Le kappa de Cohen mesure la fidélité inter-juges. Lorsque les deux juges ont un haut degré d’accord, la valeur est près de 1. Dans le cas contraire, la valeur est de 0.

Risque : ce test est utilisé pour les tableaux croisés 2 x 2. Il mesure la force de l’association entre un facteur et la fréquence d’un événement. Si l’intervalle de confiance de la statistique inclut la valeur 1, le facteur n’est pas associé à l’événement.

McNemar : il s’agit d’un test non-paramétrique pour deux variables dichotomiques. Il évalue le changement dans les réponses en utilisant la distribution Chi-2. Ce test est très utile pour détecter les changements associés à une intervention dans les devis avant-après.

Statistiques de Cochran’s et Mantel-Haenszel : cette statistique évalue l’indépendance entre une variable dichotomique indépendante et une variable dichotomique dépendante.

Une fois que vous avez sélectionné les tests Chi-2 et Phi et V de Cramer, cliquez sur POURSUIVRE.

Le bouton CELLULES

Les options qui retiennent notre attention ne sont pas les mêmes que pour le tableau croisé de la partie sur les statistiques descriptives. En effet, puisque le Chi-2 est basé sur la différence entre les occurences observées et attendues, nous sélectionnons ces deux options.

Si vous désirez calculer les occurences attendues de façon manuelle, vous cochez aussi l’option Ligne dans l’encadré Pourcentage. Vous obtiendrez les 100 % dans le sens de la variable indépendante qui est, dans notre cas, le sexe. Nous supposons en effet que le fait d’être un homme ou une femme va influencer la réponse des participants.

Les Résidus

• non standardisés illustrent la différence entre les occurences observées et attendues dans chaque cellule.
• standardisés présentent les résidus divisés par un estimé de leur écart- type. Ils ont une moyenne de 0 et un écart-type de 1.
• standardisés ajustés présentent les résidus de chaque cellule divisés par un estimé de leur erreur-type. Le résidu standardisé qui en résulte est exprimé en unités d’écart-type par rapport à la moyenne.

Dans notre cas, nous choisissons les résidus non standardisés.

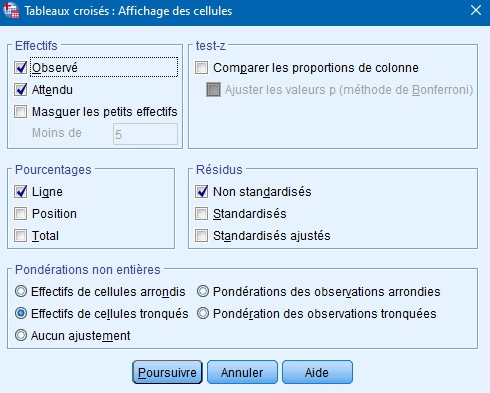
L’encadré du bas (Pondérations non entières) vous propose différentes options si les occurences dans votre tableau sont des nombres décimaux plutôt que des nombres entiers. Vous pouvez arrondir  ou  tronquer les poids des observations ou les effectifs des cellules ou même ne faire aucun ajustement.

Puisque nous avons des nombres entiers, nous n’avons pas à nous préoccuper de ces ajustements.

Vous cliquez ensuite sur POURSUIVRE.

Le bouton FORMAT

Cette boite vous donne un choix pour la présentation des rangées. Voulez-vous qu’elles soient ordonnées dans l’ordre croissant ou décroissant. Par défaut, les rangées sont ordonnées de la plus petite valeur à la plus grande.