RAPPEL THÉORIQUE
La procédure Descriptive permet de décrire la distribution d’une variable continue d’intervalle ou de rapport. Les mesures de tendances centrale et de dispersion constituent la base sur laquelle s’appuient les analyses descriptives pour ce type de variable. La procédure Descriptive ne donne pas accès à tous les indices de tendance centrale et de dispersion. Par défaut, SPSS documente la moyenne, l’écart-type, l’étendue ainsi que les valeurs minimales et maximales d’une distribution. Pour avoir une information plus complète sur une distribution, il est suggéré d’utiliser la commande Explore. Voici expliqué en détail les principaux indices qui peuvent être calculés avec la commande Descriptive.
Mesure de tendance centrale : moyenne
La moyenne arithmétique est la mesure de tendance centrale que l’on trouve le plus fréquemment dans les analyses descriptives.
Elle représente le point milieu ou le point d’équilibre des valeurs d’une variable. Elle est probablement la mesure de tendance centrale la plus employée pour les variables ordinales et continues. Elle consiste tout simplement à additionner les valeurs d’une distribution et à diviser le tout par le nombre de cas. Voici la formule de la moyenne :
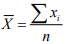
Mesures de dispersion
Les mesures de tendance centrale ne donnent pas d’information au sujet des écarts entre les valeurs, c’est-à-dire comment les données diffèrent les unes des autres. Par exemple, la moyenne et la médiane pour ces deux séries de données est 50 : 50, 50, 50, 50, 50 et 10, 20, 50, 80, 90. Cependant, les deux distributions sont complètement différentes ! Les mesures de dispersion vont tenter de quantifier l’étalement des observations.
Étendue
Mesure la plus simple de la dispersion, c’est l’intervalle complet de la distribution. Elle exprime la distance entre la borne inférieure (valeur minimale) et la borne supérieure de la distribution (valeur maximale). Plus l’intervalle est grand, plus les valeurs sont dispersées autour de la moyenne.
Variance et écart-type
La variance est la mesure de dispersion la plus utilisée. Elle est basée sur la distance au carré entre la valeur d’un cas et la moyenne de l’échantillon.
Pour y arriver, on soustrait la valeur d’un cas de la moyenne et on met au carré ce résultat. On fait la même opération pour toutes les observations.
La variance (notée S2) est la somme de toutes les distances au carré divisée par le nombre de cas moins un.
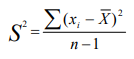
Par exemple, dans la série 28, 29, 30, 98 et 190, la moyenne est 75. La variance de cette distribution se calcule ainsi :
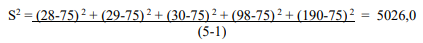
Il est possible d’obtenir un résultat dans la même échelle que la mesure originale. Il suffit de prendre la racine carrée de la variance. On obtient alors l’écart-type qui indique si la moyenne représente bien les données.
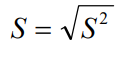
Si l’écart-type est petit, les différentes observations sont situées près de la moyenne. Dans le cas contraire, les observations s’éloignent de la moyenne.
Un écart-type de zéro signifie que toutes les observations ont la même valeur.
Coefficient de variation
La magnitude d’un écart-type dépend de l’unité de mesure. L’écart-type calculé à partir d’une donnée mesurée en jours est beaucoup plus grand qu’avec une donnée mesurée en années. De la même manière, l’écart-type de la variable « salaire » en dollars sera beaucoup plus grand que celui de la variable « âge » en années.
Le coefficient de variation exprime l’écart-type en termes de pourcentage par rapport à la moyenne. Ceci permet de comparer plusieurs variables entre elles, même si l’unité de mesure est différente pour chaque variable.
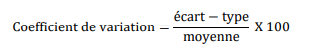
Si le coefficient égale 100 %, c’est que l’écart-type égale la moyenne.
Scores standardisés (scores Z)
L’écart-type permet d’estimer avec beaucoup plus de précision que la moyenne la position de la valeur par rapport aux autres valeurs, c’est-à-dire de positionner la valeur à l’intérieur de la distribution de l’échantillon.
Par exemple, si la moyenne de la classe est de 70 % à un examen et que l’écart-type est de 5, une note de 80 % est particulièrement bonne, car elle se situe à 2 écart-types au-dessus de la moyenne. Par contre, si l’écart-type est de 15, la note devient beaucoup moins remarquable.
Il est possible de déterminer la position relative de chaque observation en calculant ce qui s’appelle le score standardisé ou le score Z. Le calcul du score Z est simplement la valeur de l’observation moins la moyenne divisé par l’écart-type.

Le score standardisé permet de savoir à combien d’écart-type une observation se situe de la moyenne.
Dans le cas spécifique d’une distribution transformée en scores Z, la moyenne devient toujours égale à 0 et l’écart-type, toujours égal à 1. Si une observation est égale à la moyenne, son pendant en score Z sera de 0 et si une observation est égale à un écart-type au-dessus de la moyenne, son score Z sera 1.
Les scores Z négatifs représentent des valeurs sous la moyenne.