Tableau de statistiques descriptives
Le tableau montre le nombre d’observations valides pour chaque variable choisie. La ligne « N valide » représente le nombre d’observations pour lesquelles il y a une valeur valide pour toutes les variables étudiées dans la procédure.

Dans l’exemple, 1 417 participants ont donné leur âge et que 1 415 ont répondu à la question portant sur le nombre d’années de scolarité. En tout, il y a 1 413 valeurs valides lorsque les deux variables sont mises en relation. Cela signifie que ce ne sont pas les mêmes participants qui ont des valeurs manquantes pour les deux variables.
La colonne « Plage » (étendue) indique l’écart entre 18 et 89 ans, soit la différence entre la valeur minimale et maximale. Pour le nombre d’années de scolarité (educ), l’étendue est égale à la valeur maximale, puisque certains participants n’ont jamais été à l’école.
La cinquième colonne montre l’écart-type de la distribution. On observe que dans le cas de l’âge, les observations s’écartent beaucoup plus de la moyenne que dans celui des années de scolarité.
Score Z
Puisque l’on a coché l’option « Enregistrer des valeurs standardisées dans des variables » dans la boite de dialogue de la procédure Descriptives, on trouve maintenant dans la dernière colonne de la base de données une nouvelle variable qui indique les scores d’âge standardisés. Il faut déplacer la variable pour comparer plus aisément les valeurs Z avec les valeurs brutes de la variable AGE.
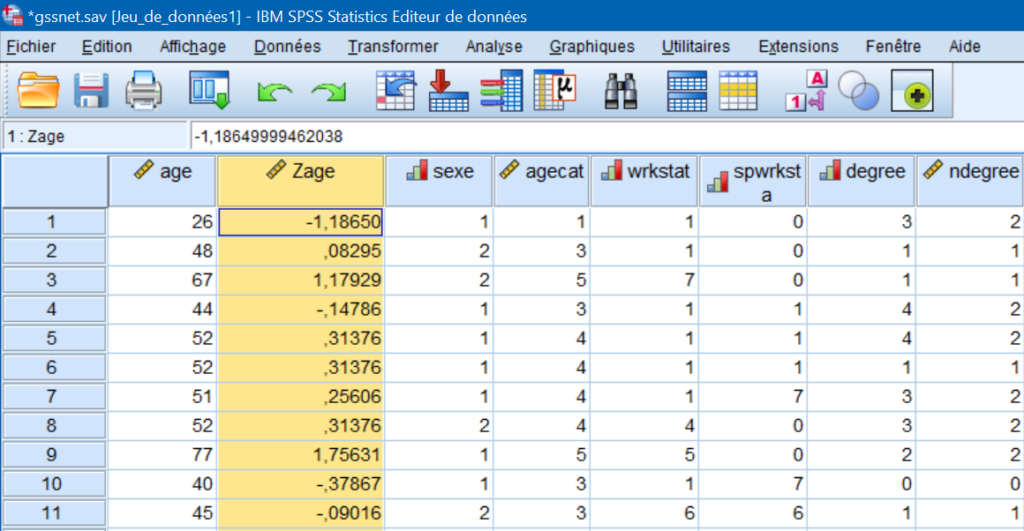
Le premier participant est âgé de 26 ans. En examinant le score Z correspondant, on peut dire que :
- cette observation est inférieure à la moyenne, en raison de la valence négative (-1,18) de la valeur Z;
- cette observation se situe à 1,18 écart-type sous la moyenne.
Le troisième participant a 67 ans. Cette valeur :
- Est supérieure à la moyenne;
- Se situe plus précisément à 1,17 écart-type au-dessus de la moyenne.
En résumé, le score Z donne deux informations essentielles sur la position d’une observation à l’intérieur d’une distribution :
- L’observation est-elle au-dessus (+) ou en-dessous de la moyenne (-),
- A quelle distance en écart- type se situe l’observation de la moyenne.
Il faut toujours porter une attention particulière aux valeurs Z très élevées (4 et plus).