Ici, nous désirions pousser plus loin l’exemple de la section précédente sur la relation entre l’espérance de vie des femmes et le taux de natalité. Nous voulions en effet savoir s’il était possible de prédire l’espérance de vie (LIFEEXPF) à partir du taux de natalité (BIRTHRAT). Pour ce faire, nous avons réalisé une régression linéaire simple à partir des données fournies dans la base COUNTRY15.SAV. Cette base comprend 15 pays de la base d’origine. Elle permet d’expliquer plus clairement la régression.

Variables introduites/éliminées

Pour la régression, SPSS ne fournit pas de statistiques descriptives à moins que vous ne les ayez demandées en cochant Caractéristiques dans la boite de dialogue des statistiques. Ainsi, le premier tableau indique les variables qui ont été introduites dans le modèle. Puisque nous avons effectué une régression simple et choisi la méthode Entrée, les deux variables choisies ont été inclues dans le modèle. Ce tableau est beaucoup plus pertinent pour la régression multiple.

Étape 1 : Évaluation de la pertinence du modèle de régression

La première chose à faire lors de l’examen des résultats est de vérifier si le modèle avec prédicteur explique significativement plus de variabilité de la variable dépendante qu’un modèle sans prédicteur. Autrement dit, il faut au préalable prendre une décision sur l’hypothèse nulle à l’effet qu’il n’y a pas de relation entre la variable dépendante et la variable indépendante. Pour prendre cette décision, il faut interpréter les résultats du tableau ANOVA.

Analyse de variance

Pour qu’un modèle soit pertinent, l’amélioration obtenue avec la variable indépendante doit être grande et les résiduels entre les valeurs observées et la droite de régression,  faibles.  Pour tester cela, SPSS procède au test de la valeur F.

Dans ce tableau, SPSS fournit les sommes des carrés et les carrés moyens dont nous avons discuté dans le rappel théorique. Le calcul de la valeur de F se fait automatiquement et le degré de signification associé se trouve dans la dernière colonne. 

Dans notre cas, la valeur de F est de 195,65 et est significative à p < 0,0005. Ceci signifie que les probabilités d’obtenir une valeur F de cette taille par hasard sont de moins de 0,05 %. Dans ce cas-ci, nous devons rejeter l’hypothèse nulle formulée plus haut. Il y a donc une relation statistiquement significative entre la variable dépendante et la variable indépendante.

Nous pouvons donc conclure que le modèle avec prédicteur permet de mieux prédire la variable y que ne le fait le modèle sans prédicteur (la moyenne de y).

IMPORTANT : Si le modèle n’apportait pas d’amélioration significative (si la valeur de F n’était pas accompagnée d’une valeur de p significative), l’interprétation s’arrêterait ici.

Étape 2 : Évaluation de l’ajustement des données au modèle de régression

Lorsque le modèle apporte une amélioration significative, on doit rapporter dans quelle mesure les données sont ajustées à ce modèle. En quelque sorte, il est possible de quantifier dans quelle mesure le modèle représente bien la dispersion des points dans le graphique.

Cette information se trouve dans le tableau « Récapitulatif du modèle » avec l’indice « R » qui présente la valeur de la corrélation multiple du modèle. La corrélation multiple (R) s’interprète de la même manière que la corrélation simple (r). Elle représente la corrélation combinée de toutes les variables indépendantes d’un modèle avec la variable dépendante. Comme nous n’avons ici qu’une seule variable indépendante, ce coefficient est identique (en valeur absolue) au coefficient de corrélation (r).

Résumé du modèle

Dans l’exemple, la valeur du coefficient de corrélation multiple est de 0,97. On trouve cette donnée sous la colonne « R ». Cette valeur suggère que les données sont très bien ajustées au modèle. 

Si nous élevons au carré le coefficient de corrélation, nous obtenons la valeur R² (0,938). Celui-ci indique la proportion de la variabilité de la variable dépendante (y) expliquée par le modèle de régression. Nous pouvons donc dire que le taux de natalité peut expliquer près de 94 % de la variation de l’espérance de vie des femmes. Remarquez qu’il est excessivement rare de trouver un coefficient aussi élevé.

La valeur de R² ajusté est un estimé de la robustesse de ce modèle si on prenait un échantillon différent provenant de la même population.

Étape 3 : Évaluation de la variabilité expliquée par le modèle de régression

Enfin, on doit rapporter la proportion de la variance totale qui est expliquée par le modèle. Cette information se situe dans le même tableau sous la colonne R-deux. Dans notre exemple, la valeur de R² est très élevée. En effet, le modèle de régression explique avec une seule variable près de 94 % de la variabilité de l’espérance de vie chez les femmes.

En dernier lieu : Les paramètres du modèle

Le dernier tableau nous donne les paramètres de l’équation du modèle de régression. Il est alors possible de construire la droite de régression à l’aide des coefficients B (Beta) non standardisés. Ce tableau est très utile dans les cas de régression multiple, car il permet de déterminer laquelle ou lesquelles des variables indépendantes contribue(nt) significativement au modèle. En effet, chaque coefficient Beta est testé en fonction l’hypothèse nulle voulant que B = 0 dans le modèle. Ceci veut dire que dans un même modèle contenant plusieurs variables indépendantes, certaines peuvent être significatives et d’autres, non significatives. Les variables significatives sont celles qui contribuent au fait que le modèle global apporte une amélioration significative de l’explication de la variabilité de la variable dépendante.

Les coefficients standardisés permettent de connaître le sens de la relation entre chaque prédicteur et la variable dépendante (relation positive ou négative) et la valeur absolue des coefficients standardisés significatifs permet de déterminer le poids relatif des variables dans le modèle.

Le prochain tableau montre donc les paramètres du modèle (les valeurs Beta) et leur degré de signification.

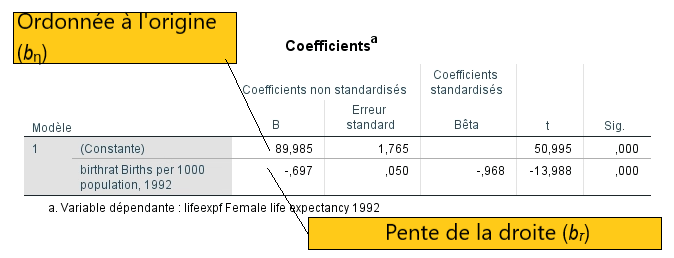
Dans le cas spécifique de notre exemple :

Les coefficients non standardisés nous permettent de reconstituer l’équation de la droite de régression. L’ordonnée à l’origine est la valeur B de la constante dans le tableau et la pente est indiquée par la valeur B pour la variable indépendante (birthrat).

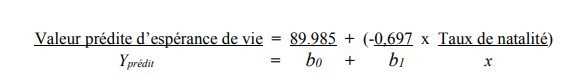
La colonne des coefficients standardisés indique la valeur du coefficient de corrélation (celle que nous avons vue dans le tableau récapitulatif du modèle). Elle apporte toutefois une nouvelle information: la valence de cette valeur (+ ou -). Il est important de connaître cette valence pour interpréter le sens de la relation entre la variable dépendante et indépendante.

La valeur actuelle du coefficient est donc de – 0,968 compte tenu de la relation négative entre les deux variables. Le dernier coefficient suggère que le modèle (la droite) de régression est très bien ajusté aux données.

La colonne suivante présente la valeur t qui teste l’hypothèse nulle à l’effet que le coefficient est égal à « 0 » dans la population. Pour l’ordonnée à l’origine, ceci veut simplement indiquer si elle est différente de « 0 ». Donc si un coefficient Beta d’une variable indépendante est significatif, son effet est différent de « 0 » et on doit l’interpréter comme une variable explicative significative. Dans le cas d’un coefficient non significatif, on doit garder l’hypothèse nulle que la valeur « 0 » est une valeur possible dans la population (t est le rapport entre la valeur Beta et l’erreur- type de mesure).

Pour notre part, nous pouvons dire que les probabilités d’obtenir une valeur t de – 13,99 si la valeur de l’ordonnée à l’origine (b) est de zéro sont de moins de 0,0005. Le b est donc différent de zéro et nous pouvons conclure que le taux de natalité contribue significativement (p < 0,0005) à prédire l’espérance de vie des femmes.