Nous nous demandons dans cet exemple si le sentiment de bonheur des participants (variable indépendante) a un effet sur leur revenu annuel (variable dépendante).

Ce questionnement est assez sommaire et quelqu’un pourrait objecter qu’il y a certainement d’autres variables associées au revenu et que la relation que nous voulons tester ne tient pas compte de l’âge des participants. 

En fait, il apparaît logique de dire que les variations (variance) du revenu sont probablement en lien avec l’âge (plus on vieillit, plus on augmente son salaire en principe). Nous allons retirer l’effet de l’âge dans la relation en le plaçant comme covariable dans le modèle.

Notre prochaine analyse répond à la question suivante : Y a-t-il toujours un effet significatif de la variable sentiment de satisfaction (HAPPY) sur le revenu (RINCDOL) une fois que l’on a contrôlé l’effet de l’âge des participants ?

Statistiques descriptives

Les principaux tableaux de résultats de l’ANCOVA sont différents de ceux obtenus avec l’ANOVA, car ils sont constitués à partir des paramètres du GLM.

Le premier tableau indique le nombre de participant dans chaque catégorie formée par la variable indépendante.

Dans notre échantillon, 227 participants se disent très heureux, 537, relativement heureux et 86, pas très heureux.

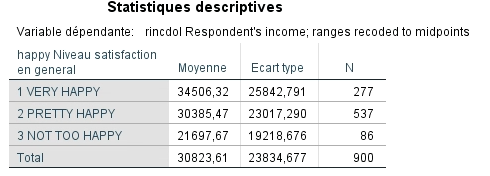
Le deuxième tableau nous donne les statistiques descriptives de la variable dépendante de l’analyse. Dans la dernière colonne, on voit encore une fois le nombre de participants dans chaque catégorie. On observe aussi le revenu annuel moyen de chaque groupe et l’écart-type qui y est associé. Ces données ressemblent à ce que l’on trouve pour l’ANOVA.

L’échantillon gagne en moyenne 30 823,61 $ par année.

Les gens très heureux semblent avoir un revenu annuel plus élevé (34 506,32 $) que les gens des deux autres groupes.

Il y a également plus de variabilité dans le revenu des gens très heureux que dans celui des gens relativement heureux et pas très heureux, puisque l’écart-type est plus grand.

Homogénéité des variances

On trouve également le tableau du test d’égalité des variances dans la procédure ANCOVA. Ce test est disponible dans les options de cette analyse.

Le test d’égalité des variances s’interprète de la même manière qu’avec l’ANOVA. 

Dans l’exemple, nous voyons que la probabilité d’obtenir une valeur F de 4,478 dans une population où les variances sont égales est de 0,01, soit 1 %. Le test est donc significatif et nous invite à rejeter l’hypothèse nulle d’égalité des variances. Nous ne respectons pas la prémisse d’égalité des variances.

Par contre, le test de Levene n’est pas le meilleur pour juger si les variances sont suffisamment différentes pour causer un problème. Une bonne deuxième vérification consiste à faire le rapport entre la variance la plus élevée et la moins élevée. Si le résultat est plus petit que 2, tout va bien. S’il est plus grand que 2, nous avons un problème. 

Dans cet exemple, le rapport est de 1,80. Nous pouvons donc poursuivre l’interprétation des résultats.

Homogénéité des droites de régression

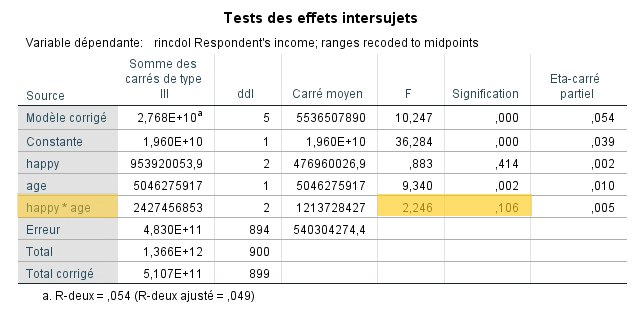
Ce tableau est semblable à celui que vous obtiendrez lorsque vous évaluerez si le modèle testé permet de rejeter l’hypothèse nulle d’absence de différence entre les groupes une fois que l’effet de la variable contrôle est retiré.

Pour l’instant, ce qui nous intéresse est la signification de l’interaction entre la variable catégorielle et la covariable. Cette interaction a été évaluée en positionnant le résultat sur dans une distribution F. Nous regardons la colonne signification et constatons que le test n’est pas significatif (p > 0,05), ce qui signifie que nous n’avons pas de preuves suffisantes pour rejeter l’hypothèse nulle d’absence de différence entre les droites de régression. Nous la conservons donc et pouvons affirmer que nous respectons cette prémisse.

Nous pouvons donc poursuivre l’interprétation des résultats.

Résultats de l’ANCOVA

C’est le tableau des tests des effets inter-sujets qui détient la réponse à la question de recherche. On y trouve les résultats des tests des effets de la variable contrôle (AGE) et de la variable indépendante (HAPPY) une fois l’effet de l’âge contrôlé.

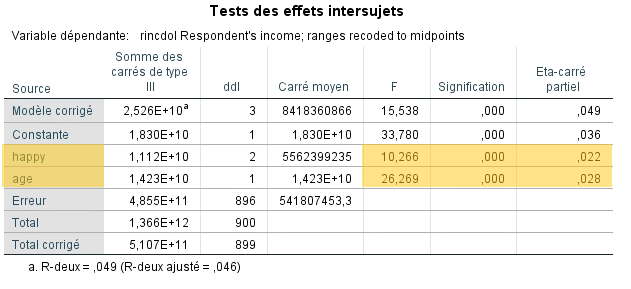
Dans un premier temps, on remarque que la variable AGE a un effet significatif sur le revenu annuel. Ces deux variables sont donc statistiquement associées et elles partagent une covariance importante (à tout le moins statistiquement significative). Nous pouvons donc dire que l’âge influence significativement le revenu annuel.

Enfin, une fois l’effet de l’âge contrôlé, il demeure un effet significatif de la variable HAPPY. On peut donc avancer que l’appartenance à un ou l’autre des groupes a un effet significatif, et ce, même en contrôlant l’effet de l’âge des participants.

Quoique la différence entre les groupes soit significative au plan statistique, la taille de l’effet associé à la variable indépendante est petite (η² = 0,02). 

Graphique

Nous savons maintenant qu’il existe une différence entre les groupes par rapport au revenu annuel. Nous ne savons toutefois pas où se situent ces différences. Nous pouvons d’abord regarder le graphique des moyennes marginales estimées.

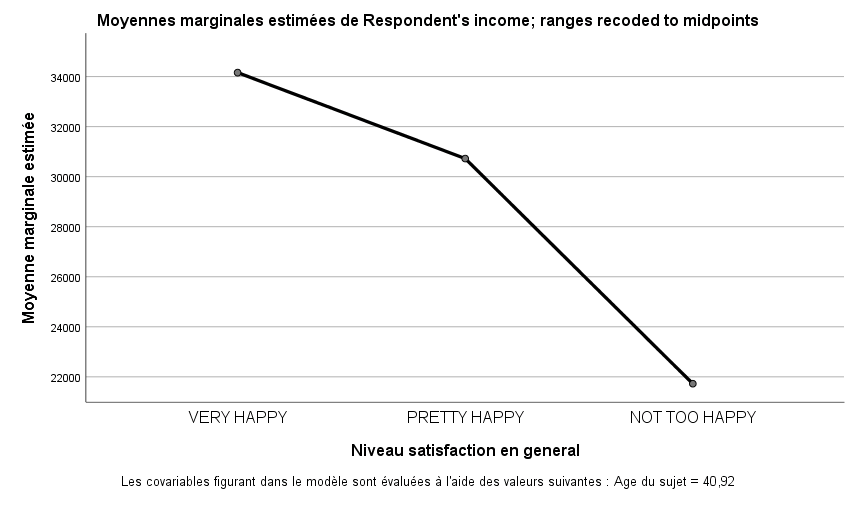
Nous constatons encore une fois que les trois groupes se distinguent au plan du revenu annuel. Nous pouvons émettre l’hypothèse qu’il existe probablement une différence significative entre les gens très heureux et pas très heureux, mais la différence est-elle également significative entre les groupes relativement heureux et pas très heureux ?

Contrastes

L’analyse de la matrice des contrastes apporte une réponse à cette question. 

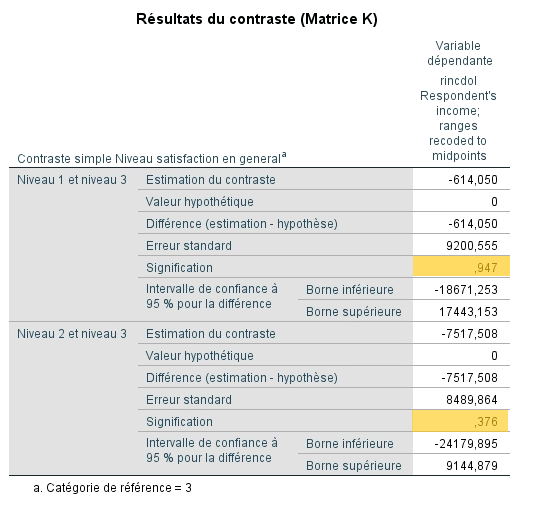
De manière assez évidente, il semble qu’il y ait des différences significatives pour les deux contrastes. La différence de revenu moyen est significative entre ce que SPSS appelle le « Niveau 1 » et le « Niveau 3 », c’est-à-dire entre le groupe Très heureux et le groupe Pas heureux. On observe une différence toute aussi significative entre le « Niveau 2 » et le « Niveau 3 », soit entre le groupe Assez heureux et le groupe Pas heureux. 

Ces différences de revenu moyen vont toutes dans le même sens, à savoir que les gens heureux bénéficient d’un revenu moyen significativement plus élevé que les gens qui ne s’estiment pas heureux.

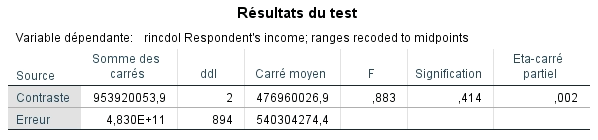
Le dernier tableau indique seulement que le test de l’analyse des contrastes est significatif, c’est-à-dire qu’il existe bien des différence entre les niveaux comparés.

Comparaisons multiples

Nous avons vu que les gens pas très heureux ont un salaire annuel moins élevé que les gens des deux autres groupes. Maintenant, existe-t-il une différence significative entre le revenu des gens très heureux et pas très heureux?

Pour répondre à cette question, nous pourrions refaire une analyse de contrastes en changeant la catégorie de référence. Il faudrait remplacer Dernière par Première.

Toutefois, pour plus de variété, nous allons regarder le tableau des comparaisons multiples obtenu à partir du bouton  dans la boite principale de l’ANCOVA.

Ce tableau s’interprète exactement de la même façon que le tableau post hoc de l’ANOVA.

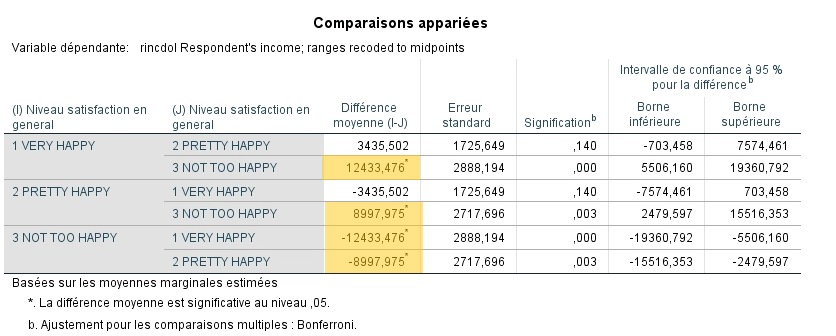
La première colonne identifie le groupe et la deuxième, les groupes comparés à celui de la première colonne. 

Dans la colonne Différence des moyennes (I- J), on observe les différences entre les groupes suivies par l’erreur-type et le degré de signification de cette comparaison.

SPSS indique par un astérisque les différences de moyennes qui sont significatives. Comme on le remarque, plusieurs comparaisons sont répétitives dans la mesure où on teste chaque groupe par rapport aux autres. Des répétitions sont inévitables. Notons que les intervalles de confiance sont aussi ajustés en fonction du nombre de comparaisons. Ils sont plus étendus que si seulement deux moyennes avaient été comparées.

Nous remarquons donc encore une fois que les gens pas très heureux se distinguent des deux autres groupes.

Toutefois, la différence entre le revenu annuel moyen des gens très heureux et relativement heureux n’est pas significative. Les gens de ces deux groupes ont donc un salaire similaire.