Comparaison de moyennes pour une variable continue
Dans l’exemple qui suit, nous nous sommes principalement intéressés à décrire la moyenne d’âge des non-utilisateurs et des utilisateurs d’Internet. La variable NETCAT contient cette information et découpe tout l’échantillon (en fait, tous les répondants ayant une observation valide pour cette variable) selon les catégories de temps d’utilisation.
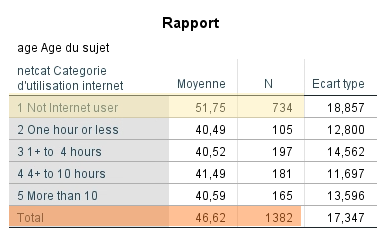
Le premier tableau indique que 1 382 participants ont donné une réponse valide à la fois à la question concernant leur âge (AGE) et à celle concernant le temps passé sur Internet par catégorie (NETCAT). Ce sont seulement ces observations qui ont été incluses dans l’analyse. Puisque 37 participants avaient des données manquantes pour une de ces deux questions (ou pour les deux), ils ont été automatiquement exclus de l’analyse.

Dans le deuxième tableau, on observe que la moyenne de tout l’échantillon (ligne Total) est de 46,62 et que cette valeur a été calculée à partir de n = 1 382.
Les 1 382 répondants ont été divisés en cinq sous-groupes qui correspondent aux valeurs possibles (donc valides) de la variable NETCAT.
Le premier sous-groupe (NETCAT = 1) contient les non-utilisateurs. On remarque que ceux-ci forment plus de la moitié de l’échantillon (n = 734) et que leur âge moyen est de 51,8.
Ce sous-groupe a en moyenne près de cinq ans de plus que la moyenne totale, alors que l’âge moyen ne varie presque pas parmi les quatre autres sous-groupes d’utilisateurs.
À partir des résultats de ce tableau, on peut affirmer que les non-utilisateurs sont plus vieux en moyenne que les utilisateurs d’Internet.
Cependant, ces résultats ne nous permettent pas de dire s’il existe une relation significative au plan statistique entre les deux variables. Rappelons-nous que nous sommes essentiellement dans un univers descriptif.
Comparaison de moyennes pour une variable dichotomique
Cet exemple est peu orthodoxe dans la mesure où l’on sait que le calcul de la moyenne s’effectue habituellement auprès d’une variable continue. Cependant, lorsqu’une variable nominale prend uniquement deux valeurs et qu’elles sont codées 0-1 (variable dite « dichotomique »), il est possible d’en faire la moyenne qui représente le pourcentage de la valeur « 1 » dans la distribution.
Dans cet exemple, nous désirions examiner l’effet de la scolarité et de l’âge sur l’utilisation d’Internet ou, plus simplement, la variation de l’utilisation d’Internet selon l’âge et le degré de scolarité. Le tableau de bord contient les moyennes de la variable USENET par catégorie d’âge (AGECAT) et degré de scolarité atteint (NDEGREE).
Puisque la variable USENET est codée 0-1, les valeurs rapportées représentent la proportion de valeur 1, donc la proportion ou le pourcentage d’utilisateurs (« 1 » étant la codification des utilisateurs).
Le premier tableau montre qu’il y avait des données manquantes pour une des trois variables pour 39 participants et des données valides pour les trois variables pour 1 380 participants. Les analyses sont réalisées à partir de ces observations.

Le deuxième tableau montre bien la ventilation de la variable AGECAT par NDEGREE. En effet, chaque catégorie d’âge est subdivisée selon les catégories de degré de scolarité.
On peut donc déterminer pour les plus jeunes (18-29 ans) le pourcentage d’utilisateurs selon le degré de scolarité atteint.
La première ligne Total donne la moyenne globale pour les 18-29 ans. On trouve une moyenne globale pour chaque catégorie d’âge. La partie inférieure du tableau donne les moyennes totales pour chaque degré de scolarité tout âge confondu. La dernière ligne Total du tableau donne la moyenne totale pour TOUT l’échantillon considéré, soit 0,47 (47 % d’utilisateurs au total).
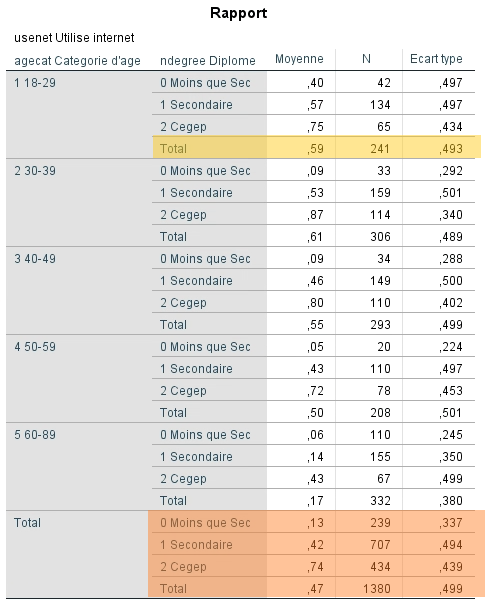
En ce qui concerne l’âge et le taux d’utilisation d’Internet, les lignes Total de chaque catégorie d’âge montrent que le taux est relativement le même parmi les quatre premières catégories (entre 0,50 et 0,61), mais qu’il est vraiment plus faible pour les 60-89 ans (0,17).
Pour la scolarité, les résultats indiquent que le pourcentage d’utilisateurs augmente toujours en fonction du degré de scolarité et que cette tendance s’observe pour toutes les catégories d’âge. Elle s’observe aussi globalement dans la partie Total du tableau. Cette ligne indique que 13 % des répondants ayant une scolarité inférieure au secondaire utilisent Internet comparativement à 42 % pour ceux qui ont complété leur secondaire et 74 % pour ceux qui ont, au moins, obtenu leur diplôme d’études collégiales.