RAPPEL THÉORIQUE

Nous allons maintenant porter notre attention sur le croisement entre deux variables continues (d’intervalle ou de rapport). Dans la perspective descriptive, nous allons examiner graphiquement cette relation. Pour les observateurs, vous remarquerez que la procédure est similaire à celle du tableau croisé dans la mesure où les variables sont croisées selon un axe vertical (colonne) et un axe horizontal (rangée).

Dans cette section, nous allons tracer le graphique dit nuage de points (Dispersion/points) qui est la meilleure représentation descriptive de la relation entre deux variables continues. Il est facile à comprendre et donne accès à plusieurs informations au simple examen visuel.

Il est toujours fortement recommandé de tracer le graphique du nuage de points avant d’entreprendre des analyses plus poussées.

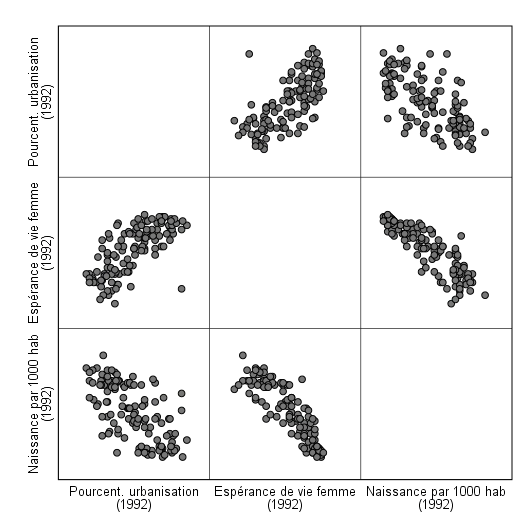
Le graphique ci-dessous illustre un exemple de nuage de points.

La figure représente l’espérance de vie des femmes en fonction (croisé avec…) du taux de natalité par 1 000 habitants. 

Chaque valeur de la variable espérance de vie (LIFEEXPF) est reportée sur l’axe vertical (axe y appelé aussi l’ordonnée), tandis que chaque valeur de la variable taux de natalité (BIRTHRAT) est reportée sur l’axe horizontal (axe x appelé l’abscisse)

Chaque point sur le graphique représente l’intersection d’un pays des valeurs combinées « taux natalité – espérance » sous la forme (x , y).  Il y a autant de points que d’observations ayant un couple de valeurs valides pour ces deux variables. 

Y a-t-il une règle pour choisir l’axe sur lequel devrait être les variables ?

Si une des deux variables est considérée comme dépendante et l’autre comme indépendante, on place habituellement la variable dépendante sur l’axe des y, c’est-à-dire en ordonnée. 

Par exemple, dans le cas d’une graphique mettant en relation le salaire annuel et le nombre d’années d’expérience, le salaire est la variable dépendante puisqu’il dépend du nombre d’années d’expérience. Il doit donc être placé sur l’axe des y.

Les sous-groupes

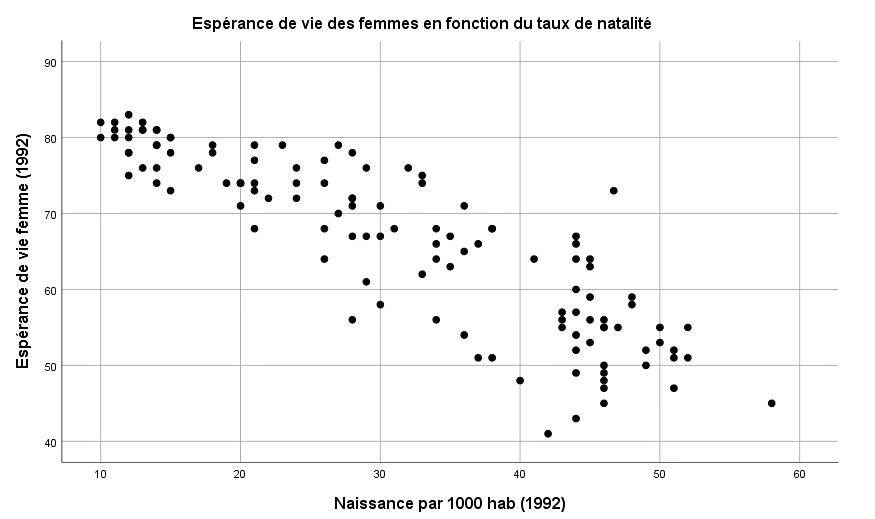
Il arrive souvent que l’on veuille savoir si la relation entre deux variables continues est la même pour différents sous-groupes de notre échantillon. On cherche à savoir si d’autres variables peuvent avoir un effet sur la relation bivariée.

Par exemple, on peut chercher à savoir si la relation entre le salaire et le nombre d’années d’expérience est la même pour les hommes et les femmes. Ou encore, si on étudie la relation entre la pression sanguine et le poids, on peut se demander si cette relation est la même pour les fumeurs et les non- fumeurs…

Une technique simple pour faire ce genre d’analyse est de marquer les points du graphique selon leur appartenance à tel ou tel sous-groupe.

Parfois, la variable marqueur est appelée variable contrôle (comme dans le cas des tableaux croisés avec strates), car en identifiant le point, on « contrôle » l’effet de la variable marqueur.

Attention : les variables marqueurs sont TOUJOURS des variables catégorielles (nominales ou ordinales)

Les regroupements 

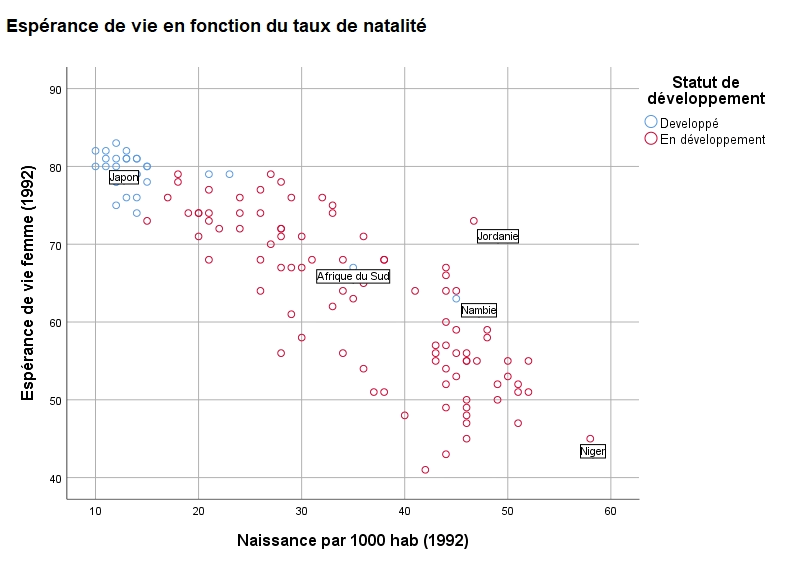
Lorsqu’il est difficile de distinguer les points parce qu’ils sont très rapprochés ou même superposés, il est possible de les regrouper en utilisant les regroupements par casiers.

La zone du graphique est alors divisée en cellules (carrées ou hexagonales) identiques en surface. Si une cellule contient un point, alors un cercle y apparaît. Si la cellule contient plus d’un point, chaque point supplémentaire fait grossir ou intensifier la couleur du groupement (cercle appelé compteur).

Matrice

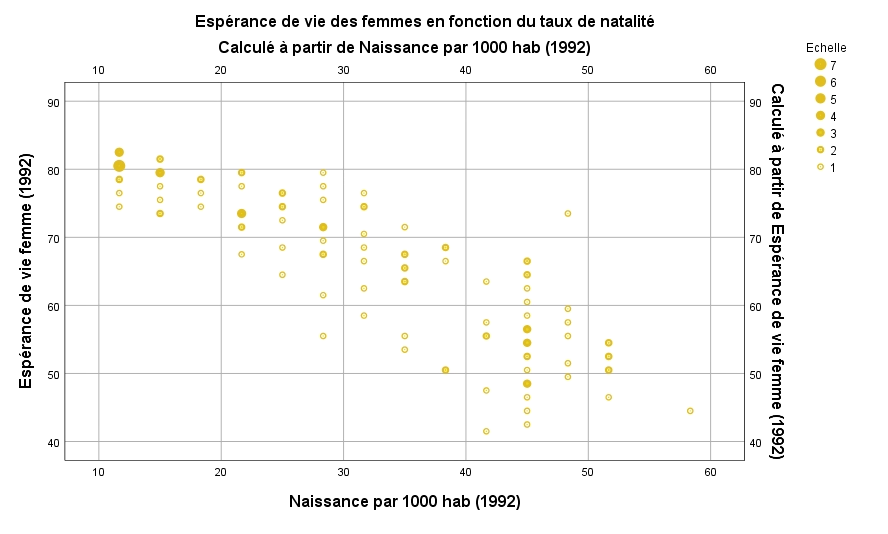
Il est possible d’examiner les relations de plusieurs variables à la fois en créant un graphique Dispersion de type matrice.

La matrice ainsi créée présente toutes les paires de variables de la liste élaborée par le chercheur. Par exemple, on pourrait s’intéresser aux relations entre le taux de natalité, l’espérance de vie et ajouter le pourcentage d’urbanisation…

La matrice ainsi obtenue contient autant de rangées et de colonnes qu’il y a de variables déclarées dans la liste.

Chaque cellule de la matrice représente le graphique de nuage de points de la paire de variables créée par l’intersection de la colonne et de la rangée.