Pour illustrer le Chi-2, nous nous basons sur la base MANIERES.SAV qui provient d’une étude faite en 1999 et qui porte sur le savoir-vivre (politesse, galanterie, maintien, etc.) dans la population américaine. 

Une des questions posées aux répondants était:

Qu’est-ce qui importe plus socialement : permettre la liberté totale d’expression même si cela ouvre la porte aux mauvaises manières ou bien promouvoir les bonnes manières même si cela limite la liberté d’expression ?

Dans cet exemple, nous voulons tester l’hypothèse nulle d’indépendance entre  les variables catégorielles SEXE et LIBERTE (variable créée par la réponse à la question précédente). L’indépendance ici signifierait que la proportion de répondants préférant la liberté d’expression serait la même pour les hommes que pour les femmes.

Statistiques descriptives

Nous observons dans le premier tableau que pour l’analyse que nous avons menée, 935 participants ont donné une réponse valide à la question citée précédemment et à celle portant sur le fait qu’ils soient un homme ou une femme. Cela représente 92,6 % de l’échantillon. Le test sera donc basé sur ces observations.

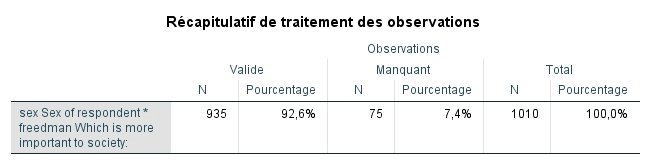
Le deuxième tableau est un tableau croisé.

On se souvient qu’il faut lire le tableau dans le sens des 100 %, donc pour chaque sexe séparément. 

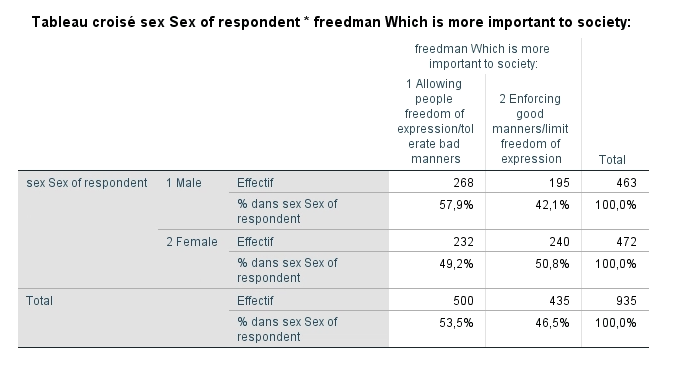
Selon le tableau, on remarque que 58 % des hommes sont en faveur de l’assurance de la liberté d’expression contre 49 % pour les femmes.  À partir de ce résultat, peut-on affirmer que les hommes et les femmes ont des attitudes différentes en regard de la liberté d’expression ? 

Dans cet échantillon, les hommes supportent davantage la première option. Nous pouvons d’ailleurs observer les différences entre les hommes et les femmes dans le graphique à barres ci-dessous.

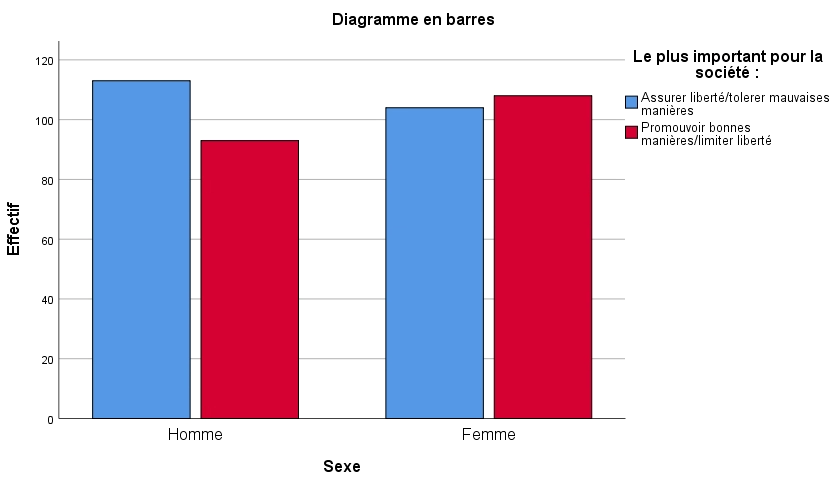
Comme à l’habitude, nous savons que ce résultat est celui d’un seul échantillon et qu’en lui-même, il est peu intéressant. Par conséquent, nous voulons  savoir ce que l’on peut conclure en regard de la population en partant des résultats de l’échantillon. Nous voulons donc tester l’hypothèse nulle selon laquelle, dans la population, le même pourcentage d’hommes et de femmes pense que la liberté d’expression est plus importante que les bonnes manières, c’est-à-dire si la variable LIBERTE est indépendante de la variable SEXE.

Nous devons donc calculer la statistique du Chi-2 à partir de la différence entre les occurences observées et attendues. Puisque SPSS peut le calculer pour nous, nous avons refait la procédure en demandant ces trois informations : les occurences observées et attendues et la différence entre les deux (résiduel non standardisé).

Nous remarquons que l’effectif théorique (ou attendu) se distingue de l’effectif observé dans l’échantillon. S’il n’y avait pas de relation entre les deux variables, l’effectif et l’effectif théorique seraient identiques.

La différence est-elle significative ? Nous pouvons évaluer le tout à partir de la statistique Chi-2.

Pour ce faire, nous devons faire la somme de chaque résidu (occurence observée – occurence attendue) mis au carré divisé par l’occurence attendue. Voici le calcul :

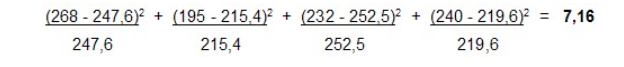
On remarque que cette formule calcule l’écart ou la distance entre l’hypothèse nulle (occurences attendues) et la situation réelle (occurences observées). La valeur de Chi-2 est une quantification de cet écart. Plus la valeur sera élevée, plus l’écart entre l’hypothèse nulle et la situation réelle sera grand.

Nous devons maintenant positionner ce résultat dans une distribution de Chi-2 ajustée en fonction du degré de liberté (nombre de rangées – 1) * (nombre de colonnes – 1). Dans ce cas-ci, le degré de liberté est 1.

La comparaison avec la distribution Chi-2 est effectuée par SPSS.

Résultat du Chi-2

Ce tableau de résultat apparaît tout de suite sous le tableau croisé. 

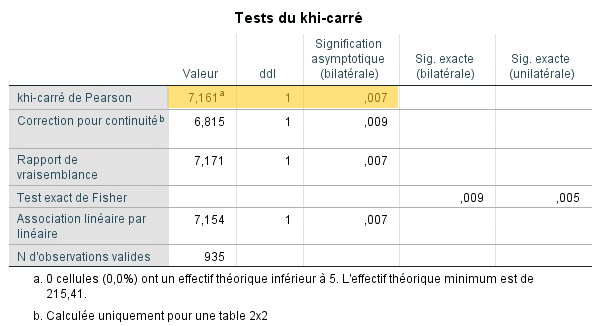
On remarque que la valeur de Chi-2 calculée par SPSS est identique à celle que nous avons calculée à la main. 

On observe aussi que le degré de signification est très bas, ce qui indique que les différences entre les occurrences observées et attendues sont significatives, ce qui veut dire que l’on retrouverait ces différences 7 fois sur 1000 si l’hypothèse nulle était vraie. 

On doit donc rejeter l’hypothèse nulle selon laquelle les femmes et les hommes répondent pareillement à la question. Il appert que les femmes préfèrent les bonnes manières significativement plus souvent que les hommes.

La dernière rangée indique le nombre d’observations valides qui ont été utilisées pour calculer la valeur du Chi-2.

Dans le bas du tableau, on voit que SPSS nous informe si nous respectons la prémisse concernant le nombre minimal d’occurences attendues par cellules. Nous voyons que dans notre cas, nous respectons la prémisse, puisque la plus petite occurence attendue est de 215,41.

Autres résultats

Correction pour la continuité : Modification de la valeur du Chi-2 seulement pour les tableaux 2 x 2. La plupart des statisticiens s’entendent pour dire que cet indice n’est pas nécessaire. On peut donc en faire abstraction.

Rapport de vraisemblance: Valeur très similaire au Chi-2. Avec des échantillons de grande taille, ces valeurs sont presque identiques.

Association linéaire par linéaire : Mesure d’association linéaire entre la variable en rangée et la variable en colonne. Cette mesure est seulement utile lors que les deux variables sont ordinales. Il faut l’ignorer dans les autres situations.

Test exact de Fisher : cette statistique apparaît uniquement pour les tableaux 2 x 2. Elle est utile lorsqu’une ou quelques cellules présentent des occurences attendues très petites. En général, ce test est moins susceptible de faire émerger des différences significatives réelles. Il est donc considéré conservateur.

La taille d’effet

Les mesures d’associations (Phi et V de Cramer) nous indiquent la force de la relation entre le sexe des participants et leur réponse à la question portant sur les bonnes manières et la liberté d’expression.

Mesures symétriques

La statistique Phi (pertinente dans le cas d’un tableau 2×2) a une valeur de 0,082 sur une valeur maximale possible de 1. Cela représente une petite association entre le sexe des participants et le fait qu’ils privilégient les bonnes manières plutôt que la liberté d’expression (si vous pensez en termes de coefficient de corrélation, cette valeur représente un effet de petite taille). La valeur du test est très significative (p < 0,01), ce qui indique que les chances d’obtenir une valeur de 0,082 par hasard est très faible. Nous confirmons donc le résultat du Chi-2 : la relation entre le sexe et la variable LIBERTE est statistiquement significative, mais de faible magnitude.