Avec la base COUNTRY.SAV, nous allons changer de sujet et nous intéresser aux relations qui existent entre l’espérance de vie des femmes, le taux de natalité par 1 000 habitants et le pourcentage de personnes vivant dans des zones urbanisées. 

L’échantillon est composé de 122 pays. Il est intéressant de noter que les sujets (les lignes) de la base de données ne sont pas des individus, mais des pays. Chaque variable possède donc des valeurs mesurées auprès d’une nation.

Nous savons que le taux de natalité et l’espérance de vie sont associés à la prospérité économique d’un pays. L’augmentation de la scolarisation, de la santé et de l’urbanisation ont eu comme effet de faire baisser le taux de natalité dans les pays industrialisés. Les études sur les pays en voie de développement suggèrent que leur taux de natalité baisse en fonction de la stagnation de leur économie.

Dans un premier temps, examinons graphiquement la relation entre l’espérance de vie des femmes (LIFEEXPF) et le taux de natalité (BIRTHRAT).

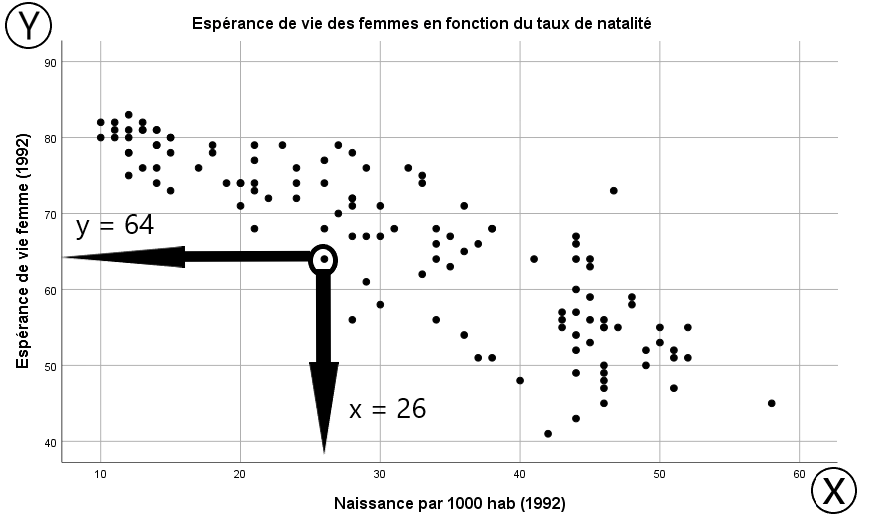
Sur le graphique ci-haut, le point encerclé représente la position de l’Indonésie. Ce pays a une espérance de vie pour les femmes (axe y) de 64 ans et un taux de natalité de 26 enfants par 1 000 habitants (axe x). La rencontre de ces deux coordonnées (x = 26, y = 64) est représentée par le point encerclé sur le graphique.

Que nous apprend le graphique de nuage de points précédent ?

Premièrement, on remarque que les points ne sont pas dispersés au hasard dans le plan. Au contraire, il semble y avoir un modèle. Les points sont concentrés dans une bande partant de la section supérieure gauche du graphique et descendant en diagonale jusqu’à la partie inférieure droite. 

Le nuage de points en forme de bande oblique donne une information très importante : plus le taux de natalité augmente, plus l’espérance de vie des femmes diminue. 

Très important : c’est une relation dite négative.

On remarque aussi que la bande exprime ce que l’on appelle une relation linéaire entre les deux variables, car la tendance générale des points peut être résumée par une ligne droite qui traverse le nuage dans le sens du modèle observé.

Une autre observation à documenter est la présence de point(s) qui s’écartent beaucoup de la bande imaginaire créée par la majorité des points. Dans le cas du graphique de l’exemple, il n’y a pas vraiment de points qui s’éloignent franchement du nuage de points.

Par contre, si un pays avait un taux de natalité de 10 enfants par 1 000 habitants et une espérance de vie de 50 ans, il faudrait examiner les données pour celui-ci pour s’assurer qu’il n’y a pas d’erreur. Prises individuellement, ces deux valeurs ne sont pas inhabituelles. Elles ne paraîtraient pas du tout anormales dans un histogramme. Ce qui serait inhabituel serait la combinaison de ces deux valeurs pour un pays spécifique.

Graphique réalisé à partir de sous-groupes

Nous voulons maintenant vérifier si la relation entre le taux de natalité et l’espérance de vie est influencée par le degré de développement du pays. Nous refaisons donc l’analyse en ajoutant une variable contrôle (DEVELOP) et nous obtenons ce graphique.

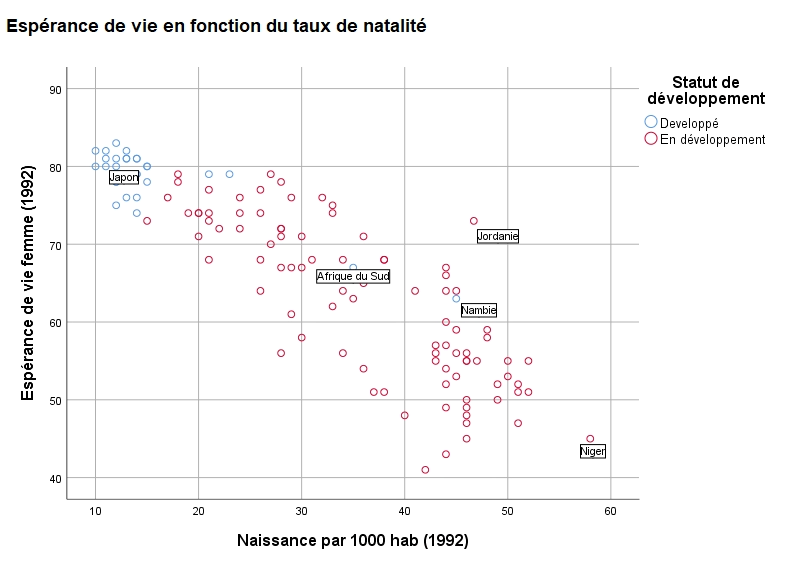
Premièrement, ce graphique est identique nuage de points précédent, à l’exception que les points (Pays) sont maintenant « marqués » par leur appartenance à un sous- groupe. 

On voit rapidement que les pays développés occupent le coin supérieur gauche du graphique et sont caractérisés par des faibles taux de natalité et une espérance de vie élevée.

Certains pays développés se distinguent toutefois de la masse. Nous les avons identifiés pour émettre des hypothèses quant à leur position dans le graphique. Israël, l’Albanie, l’Afrique du Sud et le Namibie sont des pays situés dans l’hémisphère Sud. Peut-être que le fait qu’ils sont entourés de pays en développement expliquent qu’ils aient un taux de natalité plus élevé et une espérance de vie pour les femmes moins élevée que les autres pays développés.

Les pays en voie de développement sont plus étendus en termes des deux variables. En effet, ils ont un taux de natalité variant entre 15 par 1 000 jusqu’à 60 par 1 000 habitants. Ces pays prennent la majorité de l’espace sur le graphique.

Présentation du nuage par groupements

L’exemple que nous étudions comporte beaucoup de points très rapprochés dans l’espace du graphique. Pour faciliter la lecture, nous avons créé des groupements à l’aide de la fonction regroupement.

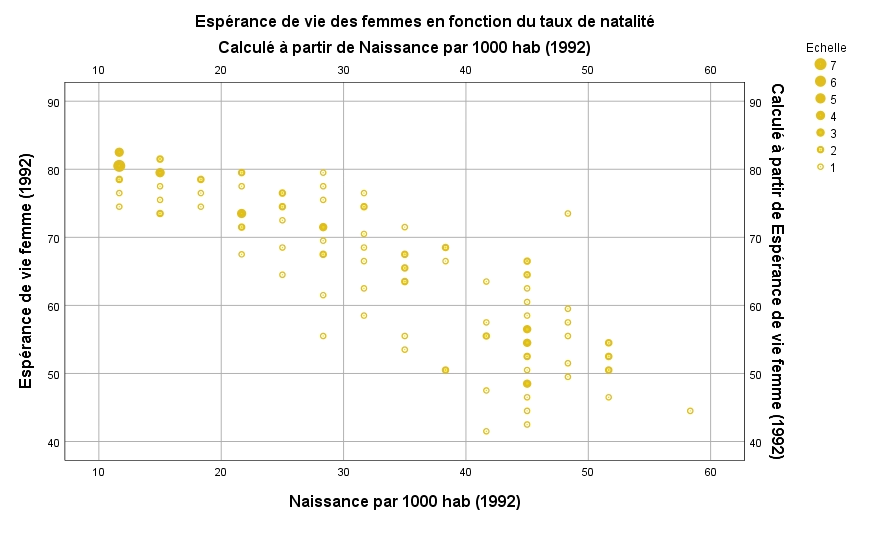
Nous voyons encore une fois le même graphique. Nous remarquons par contre que de nombreux pays ont un taux d’environ 5 naissances par 1 000 habitants et une espérance de vie pour les femmes de 80 ans. Nous savons déjà que les pays qui se définissent par ces deux caractéristiques sont développés.

Nous observons encore une fois que le Niger s’écarte des autres observations.

Matrice de graphiques de nuages de points

Puisque nous avons constaté que le fait que le pays soit développé ou en voie de développement était associé à la relation entre le taux de natalité et l’espérance de vie des femmes, nous désirions voir s’il y avait une relation linéaire entre les deux variables continues déjà étudiées et le pourcentage d’urbanisation du pays (URBAN). Nous avons donc réalisé une matrice avec ces trois variables continues.

Dans l’exemple de la matrice qui suit, la première cellule de la diagonale contient l’étiquette « Taux de natalité ». Tous les graphiques de la première rangée ont donc cette variable dans l’axe y.  De même, tous les graphiques de la première colonne ont cette variable dans l’axe x.

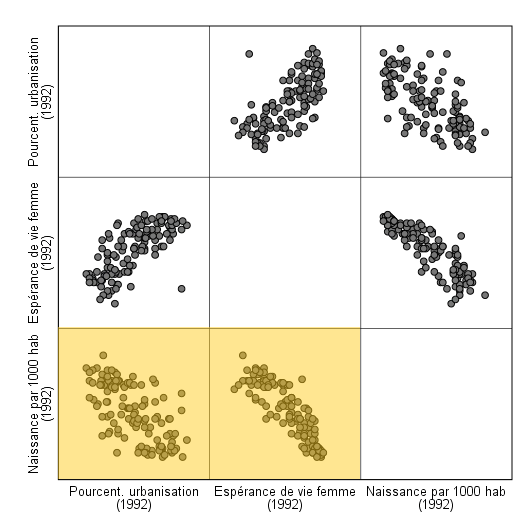
La lecture d’une matrice se fait en observant d’abord les graphiques d’une même colonne ou d’une même rangée. Se faisant, on voit en première rangée que le taux de natalité est plus fortement associé à l’espérance de vie qu’à l’urbanisation. En effet, les points sont beaucoup plus rapprochés d’une ligne imaginaire dans le graphique où l’axe x représente l’espérance de vie.

Dans la première colonne, on voit que le taux de natalité par 1 000 habitants est moins fortement associé à l’urbanisation que l’espérance de vie des femmes. Le pourcentage d’urbanisation semble donc plus influencer l’espérance de vie que le taux de natalité.

Vous pouvez aussi constater que les trois graphiques dans le coin supérieur de la matrice présentent l’inverse des graphiques dans le coin inférieur. Il est donc inutile de tous les interpréter, puisque nous avons deux fois la même information !