La technique d’estimation de l’indice alpha est relativement simple avec SPSS. Dans un premier temps, il faut s’assurer de bien identifier les items qui forment l’échelle de mesure. Dans la plupart des cas, les auteurs de l’instrument indiquent quels items font partie de quelle échelle. Notez qu’un questionnaire ou un test contient souvent plus d’une échelle de mesure.
IMPORTANT : Il est primordial d’identifier les items qui sont à recoder pour effectuer le calcul du score total. Comme SPSS calcule la matrice de corrélation inter-items, un ou des items non recodés donneront des coefficients négatifs et biaiseront le calcul de l’indice alpha. Le recodage doit donc être réalisé AVANT de procéder à l’analyse de cohérence interne. On inclut la version recodée (inversée) des items dans l’analyse.
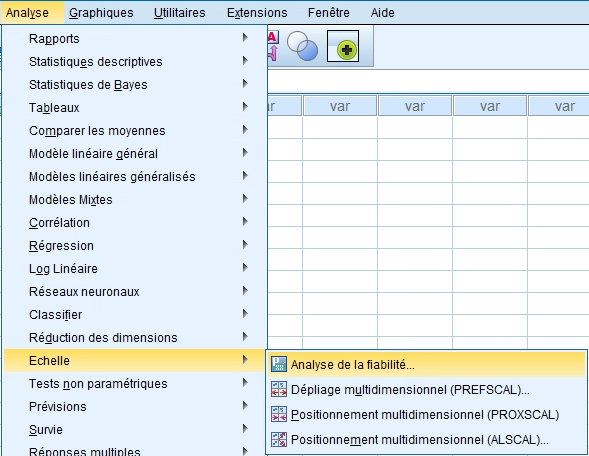
1. Dans SPSS, allez dans le menu Analyse. Ensuite, sélectionnez Échelle, puis Analyse de la fiabilité.
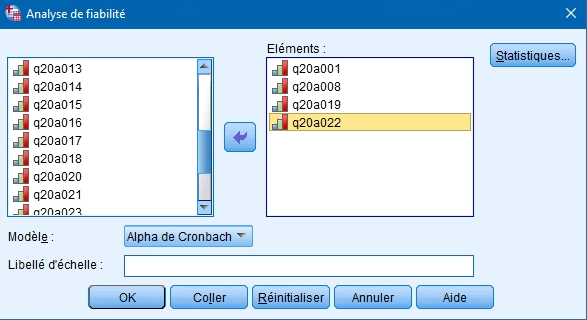
2. Vous sélectionnez les variables constituant votre première échelle de mesure dans la boite de gauche et vous les transférez dans la boite Items à l’aide de la flèche.
3. Vous pouvez effectuer plusieurs analyses de fidélité. Nous vous suggérons de conserver l’analyse par défaut, donc celle basée sur le modèle Alpha, qui est la plus utilisée.
Alpha de Chronbach :ce modèle est basé sur la moyenne des corrélations inter-items.
Split-half : ce modèle sépare l’échelle en deux et examine les corrélations entre les deux parties.
Guttman : ce modèle utilise la statistique de Guttman pour la fidélité réelle.
Parallèle : ce modèle assume que tous les items ont une variance et une erreur de variance égales à travers les différentes passations.
Parallèle stricte : ce modèle part du modèle précédent et suppose que les moyennes sont égales à travers les éléments.
Le bouton STATISTIQUES
Encore une fois, vous avez accès à plusieurs statistiques. L’encadré Caractéristiques pour est très intéressant. Il vous permet d’obtenir les statistiques descriptives pour chacun des items qui composent l’échelle (moyenne, écart-type et nombre d’observations), de l’échelle (moyenne, variance, écart-type, nombre d’éléments). La statistique la plus importante à cocher est la valeur de l’alpha pour l’échelle ans l’élément, calculée pour chacun des items retiré séparément. Vous espérez qu’aucun élément ne fait diminuer de façon importante l’indice alpha pour l’ensemble de l’échelle. Si c’est le cas, vous pouvez retirer cet élément de l’échelle.
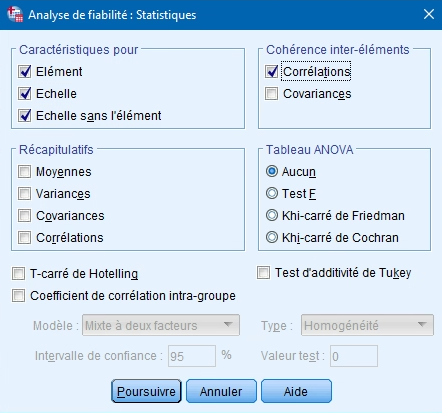
L’encadré Cohérence inter-éléments vous permet d’obtenir la matrice de corrélation entre les éléments de l’échelle ainsi que la matrice de covariance. Puisque vous vous rappelez que la matrice de corrélation présente la covariance standardisée, vous savez qu’il n’est pas nécessaire d’afficher cette deuxième matrice. De plus, la matrice de corrélation produite est identique à celle que vous avez obtenue dans l’ACP. Dans la mesure où vous n’avez pas fait d’analyse en composantes principales avant d’évaluer la consistance interne, cette matrice est intéressante puisque les coefficients de corrélation affectent directement la valeur de l’alpha.
L’encardé Récapitulatif vous propose un tableau qui résume l’ensemble du modèle. Pour la moyenne, la variance, la covariance et la corrélation entre les éléments, ce tableau comprend les informations suivantes : la moyenne, le minimum, le maximum, l’intervalle, la différence entre le minimum et le maximum, la variance et le nombre d’éléments. Vous comprendrez que la moyenne de la moyenne des éléments n’est pas une information essentielle et qu’il en va de même pour les autres statistiques de ce tableau. Par conséquent, vous n’avez pas besoin de cocher ces informations.
L’encadré Tableau ANOVA vous permet de réaliser une analyse de différence de moyennes entre les éléments de l’échelle. Vous pouvez choisir un test basé sur une distribution F pour les variables continues, le khi-carré de Friedman pour les variables ordinales ou le khi-carré de Cochran pour les variables dichotomiques. Ce test est généralement significatif même si les différences sont très faibles lorsque vous avez un échantillon de grande taille.
Enfin, dans le bas, vous avez accès à différents autres tests.
- T-carré de Hotteling : ce test vérifie l’hypothèse nulle que tous les éléments de l’échelle ont la même moyenne. Il s’agit de la version multivariée du test F de l’encadré précédent.
- Test d’additivité de Tukey : ce test évalue si certaines interactions se répètent à travers les éléments. Lorsque le test est significatif, deux éléments mesurent sensiblement la même chose.
- Coefficient de corrélation intra-classe : le calcul de ce coefficient est utile pour évaluer la fidélité inter-juge. Le détail de la procédure est très bien expliqué par Garson.
Lorsque vous avez choisi les informations que vous désirez obtenir, cliquez sur POURSUIVRE pour revenir à la boite de dialogue principale, puis sur OK pour que SPSS réalise l’analyse de consistance interne.