Tableau des statistiques descriptives

Le nombre (N) d’observations dites « valides » : une observation valide correspond à toute valeur non manquante possible pour une mesure donnée. Par exemple, lorsqu’on donne comme choix de réponse « oui » ou « non » à une question de sondage, les seules valeurs valides à cette question sont forcément « oui » et « non ».

Le nombre (N) d’observations dites « manquantes » : une observation manquante est simplement l’absence d’une valeur valide. Plusieurs raisons peuvent justifier une observation manquante. Ces personnes n’ont peut-être pas voulu répondre à la question ou encore cette dernière pouvait ne pas s’appliquer à leur situation.

Dans le cas de la variable USENET, le premier tableau montre que 1 388 participants ont répondu à la question portant sur l’utilisation d’Internet avec une des valeurs valides possibles et que pour 31 personnes, il n’y a pas de valeur valide. La somme de ces deux éléments donne toujours le nombre total d’observations de la base de données.

Tableau d’effectifs

Le titre indique le nom de la variable examinée et son étiquette (dans la mesure où elle existe).

La première colonne décrit les valeurs valides et manquantes qui ont été assignées à cette variable. Dans le cas d’une variable catégorielle (nominale ou ordinale), on voit les choix de réponses déterminés par le chercheur et leur étiquette. Ici, la variable pouvait prendre deux valeurs valides : « 0 » pour non et « 1 » pour oui. On avait également prévu la valeur spécifique « 9 » pour identifier les observations manquantes dues à l’absence de réponses de la part du participant.

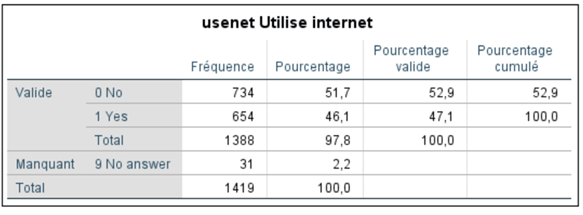
Les effectifs

La deuxième colonne indique la fréquence, l’occurrence ou encore le nombre de participants associé à chaque valeur valide spécifique (et manquante) de la variable choisie. Dans l’exemple, 734 personnes ont répondu « 0 » (No) et 654 ont répondu « 1 » (Yes), pour un total de 1 388 observations valides. En termes de valeurs manquantes, 31 personnes ont la valeur « 9 » dans la base de données.

Autrement dit, si on retourne dans la base de données et que l’on examine la colonne de la variable USENET, on pourrait compter à la main qu’il y a 734 fois la valeur « 0 », 654 fois la valeur « 1 » et 31 fois la valeur « 9 ».

Seulement les valeurs valides pour lesquelles au moins une occurrence apparaît dans la base de données sont répertoriées dans le tableau de fréquences. Autrement dit, si personne n’avait donné la réponse « No » à cette question, le tableau n’aurait pas inclus cette valeur, même si elle était un choix de réponse possible.

Le pourcentage

Le pourcentage donne la proportion de personnes pour chaque valeur possible. Ces rapports en pourcentage facilitent l’interprétation du tableau et permettent de comparer les résultats d’une étude à l’autre plus facilement.

Le calcul du pourcentage s’effectue en divisant la fréquence d’une réponse pour une valeur spécifique par le nombre total d’observations, puis en multipliant par 100.

Dans le tableau, cette information se trouve dans la troisième colonne. Les personnes qui ont répondu « Yes » représentent 46,1 % de l’échantillon (soit 654/1419 * 100), celles qui ont répondu « No », 51,7 % (soit 734/1419 * 100) pour une proportion totale d’observations valides de 98,7 %. Il y a donc 2,2 % d’observations manquantes (soit 31/1419 * 100).

La somme de toutes les proportions des réponses avec les manquantes donne toujours 100 %.

Le pourcentage valide

Les pourcentages de la colonne « Pourcentage » sont difficilement interprétables parce qu’ils considèrent à la fois les réponses valides (98,7 %) et manquantes (2,2 %).

Pour trancher la question, la colonne « Pourcentage valide » affiche les pourcentages relatifs uniquement pour les sujets ayant donné une réponse valide. 

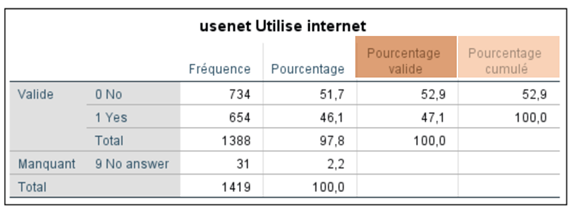
Dans ce cas, le tableau montre que 52,9 % des répondants utilisent Internet seulement pour le courriel et que 47,1 % s’en servent pour d’autres fonctions.

Le pourcentage cumulé

La dernière colonne de la table de fréquence permet de calculer le cumul des pourcentages des catégories précédentes à partir de la première. Donc, on calcule que la proportion des utilisateurs qui se servent d’Internet seulement pour le courriel et ceux qui l’utilisent pour d’autres fonctions représentent 100 % des personnes qui ont donné une réponse valide. L’interprétation de cette colonne fait du sens lorsqu’il s’agit d’une variable ordinale ou lorsqu’il est pertinent de cumuler des catégories. Par conséquent, pour une variable dichotomique (oui/non), l’interprétation est moins pertinente.

Un autre exemple

Le tableau porte cette fois sur la variable NETCAT qui évalue, par catégories, le nombre d’heures passées sur Internet.

Le pourcentage valide

On observe que 54,3 % des répondants ne sont pas des utilisateurs d’Internet (51,7 %) ou n’ont pas répondu (2,5 %). 

On lit aussi qu’environ 12 % de l’échantillon utilise Internet 10 heures ou plus par semaine.  Ce pourcentage peut représenter une petite portion des répondants si peu de participants utilisent Internet ou si la majorité des utilisateurs s’en sert moins de 10 heures par semaine. 

Il est donc intéressant de regarder la colonne « Pourcentage valide ».

Dans ce cas, le tableau montre que parmi les utilisateurs d’Internet, 25,4 % s’en servent plus de 10 heures par semaine. Notez qu’il a fallu recoder la valeur « 1 » comme valeur manquante sous l’onglet Affichage des variables.

Le pourcentage cumulé 

La dernière colonne montre que la proportion des utilisateurs passant 4 heures et moins sur Internet est de 46,7 % (16,3 % + 30,4 %). De même, on peut dire qu’au total, les utilisateurs passant 10 heures et moins sur Internet représentent 74,6 % des utilisateurs (16,3 % + 30,4 % + 27,9 %).