Dans cet exemple, nous allons reprendre les étapes présentées dans le rappel théorique pour réaliser une analyse en composantes principales. Nous utilisons la base PCA exemple qui comprend des données provenant d’une étude sur la clientèle des centres jeunesse du Québec (Pauzé et al., 2004). Les données portent sur un questionnaire évaluant les ressources disponibles (logement, argent, soutien social, etc.) pour les participants de l’étude. Ce questionnaire comprend 28 items auxquels les 231 participants ont répondu à l’aide d’une échelle de type Likert. Voici un exemple d’items du questionnaire:

Étape 1: Déterminer l’approche selon le type de problème
Nous adoptons l’approche exploratoire, car nous n’avons pas d’idées préalables sur la structure des données.
Étape 2: Préparation de l’analyse
| Nombre de variables | Nous réalisons notre analyse sur 28 variables. Nous croyons que nous serons en mesure de faire émerger des construits latents et de réduire de façon intéressante le nombre de variables originales. |
| Type de variables | Puisque les réponses sont basées sur une échelle de type Likert, les données sont continues. |
| Taille de l’échantillon | 231 personnes ont répondu au questionnaire. Nous dépassons le minimum de 100 participants au total, mais pas celui de 10 personnes par variable tel que recommandé par Hair et al. (1998). Pour atteindre le nombre requis, il aurait fallu avoir 280 répondants (28 questions x 10). Nous continuons tout de même l’analyse. |
Étape 3: Respect des postulats
Nous nous assurons ensuite de respecter les postulats avant de procéder à l’analyse proprement dite.
Corrélations inter-items
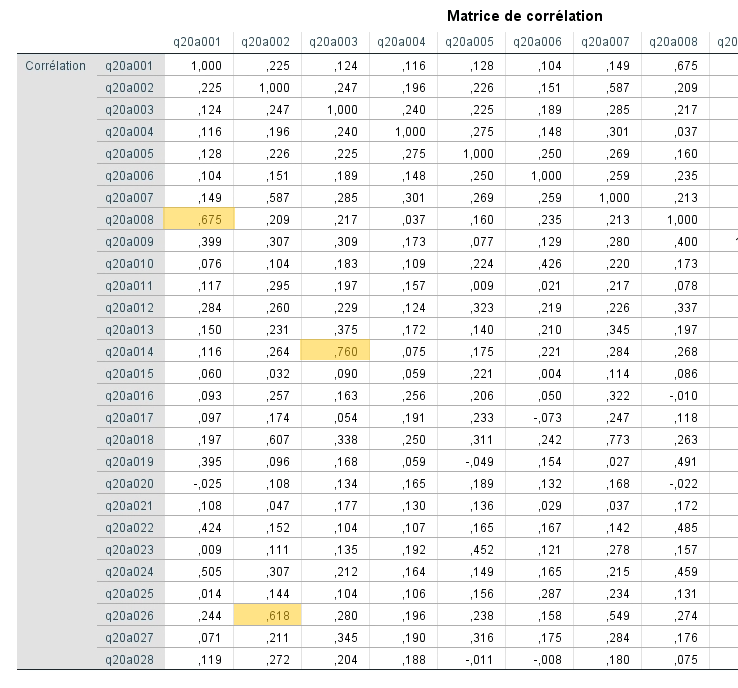
D’abord, nous devons nous assurer que les items sont minimalement corrélés entre eux. Pour ce faire, nous regardons la matrice de corrélation. Dans ce détail de la matrice, nous pouvons observer que toutes les variables semblent au moins légèrement corrélées. Certaines corrélations sont plus fortes que d’autres, nous suggérant déjà quelques associations.
Mesure de l’adéquation de l’échantillonnage (KMO) et Test de sphéricité de Bartlett
L’indice KMO de 0,81 peut être qualifié d’excellent ou de méritoire. Il nous indique que les corrélations entre les items sont de bonne qualité. Ensuite, le résultat du test de sphéricité de Bartlett est significatif (p < 0,0005). Nous pouvons donc rejeter l’hypothèse nulle voulant que nos données proviennent d’une population pour laquelle la matrice serait une matrice d’identité. Les corrélations ne sont donc pas toutes égales à zéro. Nous pouvons donc poursuivre l’analyse.

Étape 4: Choix de la méthode d’extraction
Nous choisissons l’analyse en composantes principales, puisqu’elle permet d’expliquer une grande partie de la variance avec un minimum de facteurs.
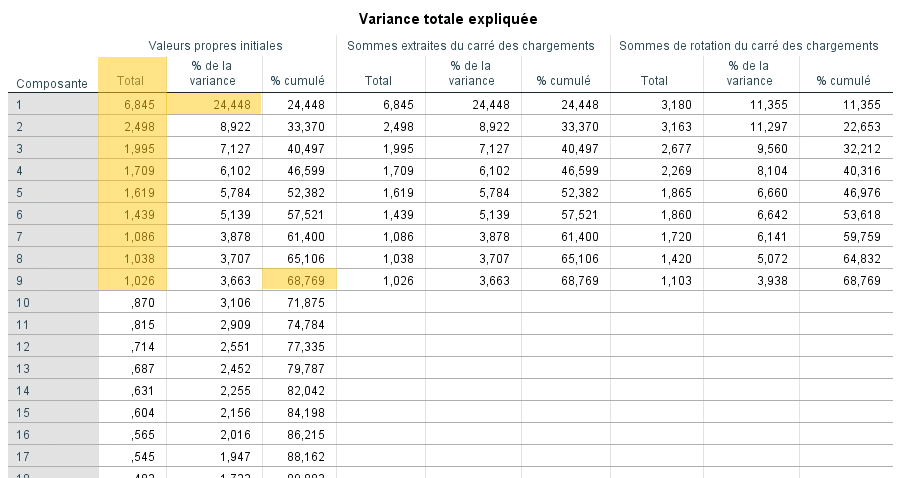
Nous devons ensuite choisir le nombre de facteurs à extraire. Pour ce faire, nous analysons le tableau de la variance totale expliquée. En regardant la deuxième colonne, nous constatons que neuf facteurs (ou composantes) ont une valeur propre plus élevée que 1. Nous les conservons donc pour l’analyse. Le premier facteur explique à lui seul 24,45 % de la variance totale des 28 variables de l’analyse. Mis en communs, les neuf facteurs permettent d’expliquer 68,77 % de la variance. Comme les facteurs 10 à 28 n’expliquent pas suffisamment de variance, ils ne sont pas retenus.
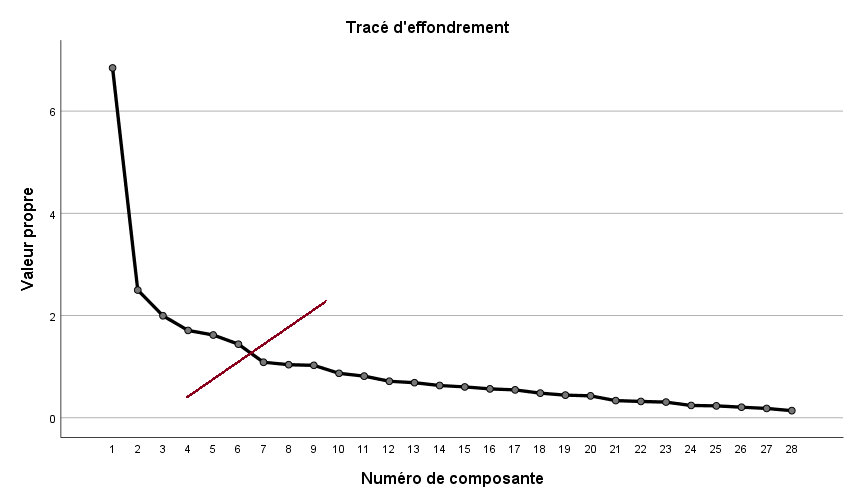
Nous désirons toutefois être certains de bien choisir le bon nombre de facteurs à extraire. Nous regardons donc le graphique des valeurs propres et examinons où se situe la rupture du coude de Cattell. Nous voyons un changement après le sixième facteur. Nous ne retenons donc que six facteurs pour l’analyse, puisque ce critère est plus rigoureux que celui des valeurs propres.
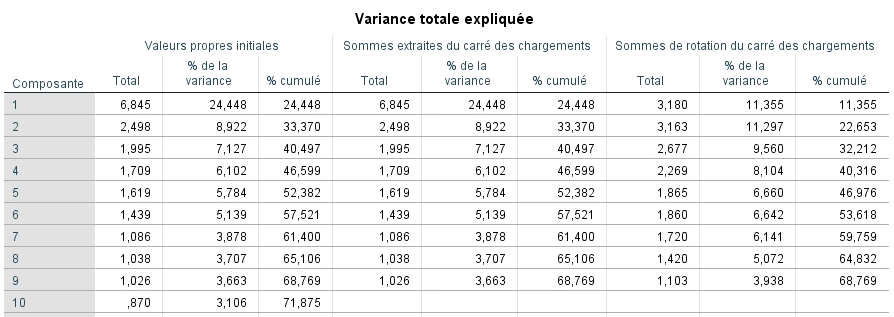
Puisque nous avons retenu seulement six facteurs, nous avons refait l’analyse en spécifiant que nous désirions conserver ce même nombre de facteur dans la boite de dialogue d’extraction. Nous pouvons à nouveau regarder la matrice de la variance totale expliquée. En fait, la seule différence est que SPSS ne fournit pas les détails des facteurs 7 à 9. Avec nos six facteurs, nous pouvons expliquer 57,52 % de la variance totale.
Étape 5: Interprétation des facteurs
Nous voulons maintenant déterminer la combinaison de variables qui est la plus associée à chacun des facteurs significatifs. Nous allons procéder en trois étapes.
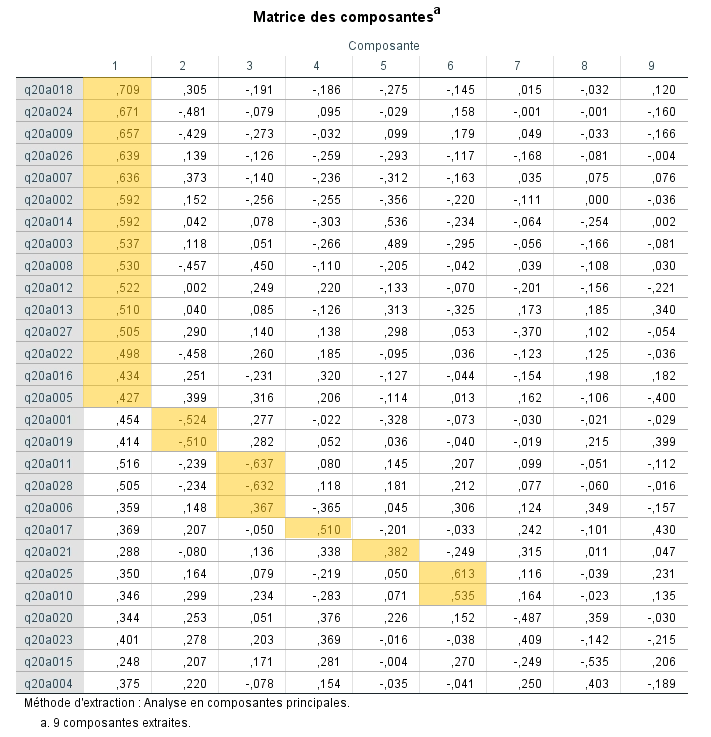
1. Examen de la matrice des composantes (sans rotation)
Avant de faire la rotation, nous observons que 17 variables saturent plus fortement sur le facteur 1 et permettent par conséquent de le définir. Entre une et trois variables saturent sur les autres facteurs. Nous observons également que certaines corrélations se ressemblent étrangement d’un facteur à l’autre. Par exemple, la question 6 obtient une corrélation de 0,367 sur le facteur 3 et de – 0,365 sur le facteur 4. Il est donc difficile d’établir quelles variables vont réellement avec quel facteur.
2. Examen de la matrice des composantes après rotation et
3. Identification du poids le plus élevé pour chaque variable
Afin d’obtenir une représentation factorielle plus simple, nous faisons une rotation VARIMAX. Ce type de rotation permet de préserver l’orthogonalité (l’indépendance) entre les facteurs. Nous notons cette fois que les variables sont beaucoup mieux réparties sur les différents facteurs. De plus, l’écart entre les corrélations est plus élevé une fois que la rotation a été effectuée. Puisqu’au moins trois variables saturent sur chacun des facteurs, nous pourrons les conserver pour construire des échelles.
Nous remarquons aussi que certaines variables saturent de façon importante sur plus d’un facteur. Ceci signifie qu’il faudrait probablement retirer ces variables qui ne se positionnent pas de façon adéquate sur un seul facteur et recommencer l’analyse. Toutefois, puisque nous ne voulons ici que vous présenter la démarche, nous allons poursuivre l’analyse.

4. Étiqueter les facteurs
Nous devons maintenant nommer les facteurs et tenter d’identifier le construit latent qu’ils permettent de mesurer. Si nous prenons, par exemple, le facteur 1, nous avons les questions suivantes:
1. J’ai assez de temps pour mes activités de loisir.
8. J’ai assez de temps pour faire les choses que j’ai envie de faire.
19. J’ai suffisamment de temps pour le travail domestique.
22. J’ai suffisamment de temps pour aider les autres.
24. J’ai assez d’énergie pour mes loisirs.
Nous voyons que la notion de temps revient dans les quatre premières questions. Nous pourrions nommer ce facteur « temps disponible ». Probablement que finalement, la dernière question va un peu moins avec ce facteur. Il est vrai que si nous regardons sa corrélation sur le facteur 1 et sur le facteur 4, nous constatons qu’il n’y a pas tellement de différence entre les deux: 0,618 et 0,531. En réalité, nous espérons qu’après la rotation, il y aura au moins 0,3 points de différence entre la corrélation entre la variable et son facteur et sa corrélation sur les autres facteurs. Par conséquent, nous pouvons penser à éliminer cette variable de l’analyse.