RAPPEL THÉORIQUE

Nous venons de voir comment construire une échelle à partir des facteurs qui ont émergé de l’ACP. Nous allons maintenant vérifier si notre échelle est suffisamment fidèle pour être utilisée dans un questionnaire.

Cette dernière partie traite donc d’une technique statistique qui n’est pas dans la famille des statistiques inférentielles, mais qui est largement utilisée et présentée dans les études sur les propriétés psychométriques d’un instrument de mesure et plus précisément des instruments qui évaluent un ou des construits à l’aide d’échelles de mesure.

Par définition, une échelle de mesure est un ensemble d’éléments portant sur le même construit et dont la somme (ou la moyenne) représente la « quantité » du construit pour un sujet donné. Une caractéristique fondamentale de l’échelle de mesure est que l’on répond à tous les éléments qui la composent à l’aide d’une échelle de type Likert, soit un choix de réponse gradué allant, par exemple, d’une fréquence moindre à une fréquence élevée (1= jamais, 2= quelques fois, 3= souvent et 4= toujours). Il est également possible d’avoir une échelle de mesure composée d’items dichotomiques (0-1).

Nous allons nous intéresser ici à un aspect important de la fidélité d’une échelle de mesure. La fidélité est considérée, entre autres, comme 1) la propriété d’une mesure à être stable dans le temps pour un même sujet (fidélité test-retest) et 2) la propriété d’une mesure à être constante dans l’objet mesuré (homogénéité). Autrement dit, pour être fidèle, une échelle de mesure doit retourner un même score pour une même personne lorsque celle-ci remplit le questionnaire à des moments différents dans le temps, mais elle doit aussi être composée d’items qui mesurent tous le même construit.

À cet égard, une des propriétés psychométriques importante à estimer lorsque l’on s’intéresse à ce type de fidélité est l’homogénéité des éléments de l’échelle de mesure, mieux connue sous le nom de consistance ou cohérence interne. 

On dit d’une échelle qu’elle est cohérente ou homogène lorsque tous ses éléments convergent vers la même intensité de réponse. En d’autres mots, plus les réponses aux éléments sont corrélées entre eux et au score total de l’échelle, plus la cohérence de cette échelle est élevée. Au contraire, si les scores de plusieurs éléments vont dans le sens contraire du score total, on peut douter de la cohérence de cette échelle.

À cet égard, la technique d’estimation de l’homogénéité des items d’une échelle est basée sur le patron de corrélations des items entre eux ainsi qu’entre eux et le score total. Plus l’homogénéité est grande, plus l’échelle est fidèle au sens de la cohérence interne des items, plus on peut croire que les items mesurent un seul et même construit. Également, plus l’homogénéité est élevée, plus les items mesurent le « vrai score » de l’individu, diminuant ainsi l’erreur de mesure qui fait varier le score total d’une mesure à l’autre dans le temps.

Méthodes d’estimation de la cohérence interne d’une échelle

Il existe plusieurs façons d’apprécier la cohérence interne d’une échelle. Nous allons passer rapidement sur les premières pour nous attarder spécifiquement sur la méthode la plus utilisée, soit le calcul de l’indice alpha de Cronbach.

Matrice de corrélation inter-items

Imaginons une échelle comprenant 6 éléments mesurés à l’aide d’un choix de réponses à 5 valeurs. Une manière rapide d’estimer la cohérence interne de ces éléments est de simplement examiner la matrice de corrélation des éléments entre eux. Ceci donnerait un total de 15 coefficients de corrélation.

Dans l’exemple ci-dessous, on pourrait calculer la corrélation moyenne en faisant simplement la moyenne des 15 coefficients. Ici, cette moyenne serait de 0,90 avec des valeurs individuelles variant entre 0,84 et 0,95. Cet indice élevé suggère une forte homogénéité des items de l’échelle

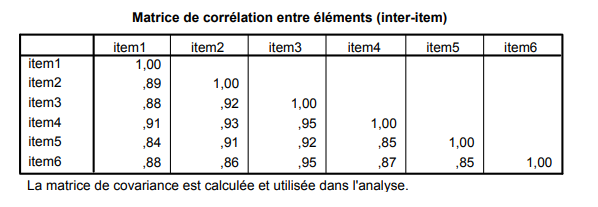
Matrice de corrélation item-total

On pourrait également mettre en relation chaque élément avec le score total de l’échelle pour évaluer le degré d’association entre chaque élément et le score total. Cette démarche est intéressante, car elle s’approche de notre définition de la cohérence interne…

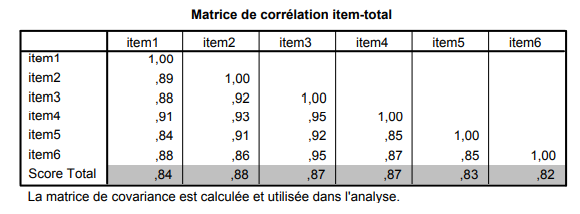
En reprenant l’exemple précédent et en ajoutant le score total, on peut facilement faire la moyenne des coefficients de corrélation de chaque élément avec le score total ce qui donne ici 0,85.

Méthode split-half

Cette méthode consiste à séparer aléatoirement les éléments en deux groupes contenant le même nombre d’éléments. Par la suite, on calcule le score partiel de chaque groupe d’éléments pour chaque individu pour enfin calculer la corrélation entre les deux scores partiels.

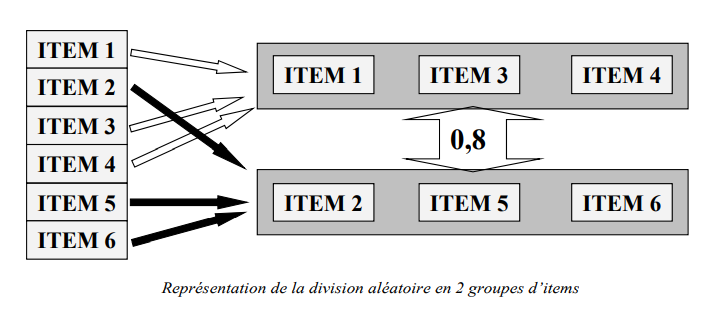
Calcul de l’indice alpha de Cronbach

Imaginez que nous recommencions la méthode split-half avec des regroupements différents d’éléments jusqu’à ce que nous ayons calculé les coefficients de corrélation de TOUS les regroupements différents possibles.

L’indice alpha de Cronbach (représenté par la lettre grecque « α ») est l’équivalent mathématique de l’estimé split-half moyen de TOUS les estimés split-half possibles. Cette procédure se fait en gardant le même échantillon et non en sélectionnant un nouvel échantillon pour chaque combinatoire split-half. Avec une échelle de 100 éléments, imaginez le nombre d’échantillons que vous devriez créer !

M. Cronbach a concocté une formule qui permet de faire l’approximation en un seul calcul. L’indice résultant est une expression décimale qui varie entre 0 et 1. Plus la valeur alpha s’approche de 1, plus l’ensemble d’éléments est homogène. 

Dans la formule, N correspond au nombre d’éléments dans l’analyse et r représente le coefficient inter-items moyen. Il faut noter que la formule proposée est celle de l’indice alpha standardisé. 

On peut constater à partir de la structure de la formule que plus une échelle comporte d’éléments, plus l’indice alpha de Cronbach risque d’augmenter. De même, une faible corrélation inter-items fera diminuer l’alpha, tandis qu’une corrélation inter-items élevée le fera augmenter. 

Ceci fait bien du sens dans la mesure où des éléments fortement corrélés entre eux indiquent vraisemblablement la mesure d’un même construit et c’est exactement ce que l’on veut dire lorsque l’on dit d’une échelle qu’elle possède une bonne ou une mauvaise cohérence interne. 

Ceci fait référence également à l’idée qu’une échelle mesure un construit sous-jacent qui est unidimensionnel. En effet, si les éléments qui constituent l’échelle mesurent plus d’un construit (multidimensionnel), l’indice alpha sera probablement très bas.  

Pour bien faire les choses, le chercheur devra regrouper et séparer les éléments en fonction du construit mesuré et refaire le calcul de l’indice alpha pour chaque ensemble d’éléments.