RAPPEL THÉORIQUE
Dans cette section, nous nous intéressons à la vérification d’hypothèse pour un échantillon dont les répondants ont été évalués deux fois à partir de la même mesure (donc deux moyennes). Lors de l’évaluation d’un programme d’intervention, les chercheurs peuvent utiliser ce test pour comparer les résultats obtenus par les participants au pré-test et au post-test. Puisque les moyennes proviennent des mêmes individus, elles sont appelées moyennes dépendantes.
Hypothèse nulle
Il n’y a pas de différence entre les valeurs des deux moyennes dans la population. En d’autres termes, la différence entre les deux moyennes dans la population est de 0 (par exemple, les scores avant et après l’intervention sont les mêmes pour le même individu).

L’hypothèse alternative est qu’il existe une différence.
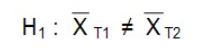
Prémisses du test t pour échantillons appariés
La distribution des deux mesures est normale dans la population OU l’échantillon est assez grand pour permettre de référer au théorème central limite pour la normalité de la distribution échantillonnale des différences de moyennes.
Les deux mesures sont des variables continues possédant la même échelle de mesure.
Test-t pour échantillons appariés
Souvent, le but de ce test est de vérifier l’effet de la variable indépendante (une intervention) sur la variable dépendante (les sujets, ces derniers ayant été pairés d’une façon ou d’une autre). On mesure donc la variable dépendante avant et après l’intervention.
Le test-t pour échantillons appariés peut aussi être utilisé pour des sujets qui ont été exposés à deux conditions expérimentales.
L’avantage de ce devis est qu’il est plus facile d’attribuer les différences de taux à l’effet de l’intervention lorsque les mesures sont pairées. Si on observait deux groupes distincts (un qui a l’intervention et un qui ne l’a pas), les différences observées seraient peut-être dues aux différences inhérentes entre les deux groupes au départ.
Le test t pour échantillons appariés compare les sujets avec eux-mêmes. Ceci permet de détecter les différences si elles existent bel et bien.
Calcul des différences
Dans ce type de test, notre intérêt porte sur les différences de moyennes qui existent entre les deux variables mesurées pour le même individu ou pour la paire d’observations.
La valence de cette différence en indique le sens. Si on effectue une mesure avant et après l’observation et que le résultat du test est positif, ceci signifie que le score après est plus élevé que le score avant, et vice versa.
S’il n’y a pas de changement réel, on s’attend à observer le même nombre de valeurs positives et négatives.
Au delà de la signification statistique : la taille de l’effet
Le test t nous donne un résultat important : il nous informe si la différence observée entre les deux mesures est statistiquement significative, donc si elle n’est pas simplement due au hasard.
Toutefois, cette différence significative en termes statistiques peut être insignifiante en termes cliniques. En effet, lorsque des échantillons imposants sont comparés, il est possible de détecter une différence significative de moyennes même avec de très petits écarts entre les mesures.
Il nous faut donc un moyen pour apprécier l’importance de la différence de moyennes. Une façon largement utilisée est de recourir au calcul de la taille de l’effet (effect size) qui fait référence à la force ou à la magnitude de l’association.
Tabachnick et Fidell (1996) définissent la taille de l’effet comme « la proportion de la variance totale de la variable dépendante qui est expliquée par la connaissance des niveaux de la variable indépendante ».
On parle aussi de la distance entre H0 et H1.
Cohen (1988) explique différentes façons de calculer la taille de l’effet (le d et le f de Cohen) dont la plus commune est le calcul de l’eta-carré partiel (η2) (partial eta squared) qui est fourni par SPSS pour l’ANOVA et plusieurs autres techniques d’analyses multivariées. Bien que cet indice ne soit pas disponible pour le test t, il est possible de le calculer aisément à la main avec la formule suivante :
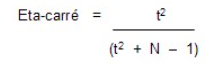
L’eta-carré représente donc la proportion de variance de la variable dépendante (la variable testée) expliquée par la variable indépendante (la variable groupe). Cet indice varie entre 0 et 1 et les balises suivantes ont été élaborées par Cohen (1988) pour guider son interprétation.
